1) x²+y²-10*x+9=(x²-10*x)+y²+9=[(x-5)²-25]+y²+9=(x-5)²+y²-16=0, откуда (x-5)²+y²=16=4² - это уравнение окружности с центром в точке O(5;0) и радиуса R=4.
2) Уравнение эллипса имеет вид x²/a²+y²/b²=1, где a и b - большая и малая полуоси эллипса. Фокусное расстояние эллипса c=[7-(-7)]/2=7. Так как b²=a²-c² и e=c/a, то a=c/e=7/0,28=25 и тогда b=√(a²-c²)=√576=24. Поэтому уравнение эллипса таково: x²/625+y²/576+1.
3) Уравнение параболы задано в форме y²=2*p*x, откуда p=8/2=4 - расстояние от фокуса до директрисы параболы. Поэтому директриса имеет уравнение x=-p/2=-2, а абсцисса фокуса x0=x+p=x+4=2. Поэтому фокус имеет координаты (2;0.
cм. рис.
Пошаговое объяснение:
кубическая парабола, снизу-вверх.
Взять производную,
исследовать f'(x) на f'(x) < 0, f'(x) > 0
определить экстремумы.
f'(x) = 3x² - 5x - 2
f'(x) = 0 при
3x² - 5x - 2 = 0
D = 25 - 4 * 3 * (-2) = 49 - 7²
x1 = (5-7) / 6 = -1/3
x2 = (5+7) / 6 = 2
f'(x) = 3x² - 5x - 2 (роги вверх => меньше нуля - между корнями)
f'(x) < 0 при x ∈ (-1/3; 2) => f(x) убывает
f'(x) > 0 при x ∈ (-∞; -1/3) ∪ (2; +∞) => f(x) возрастает
х1 - точка максимума
х2 -точка минимума
f(-1/3) = (-1/27) - (5/2)*1/9 - 2*(-1/3) + 3/2 = -1/27 - 5/18 + 2/3 + 3/2 =
= -1/27 + (-5 + 12 +27)/18 = -1/(9*3) + 34/(9*2) = (-2+102) / (9*3*2) =
= 100/54 =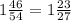 (почти 2)
(почти 2)
f(2) = 8 - 10 - 4 + 3/2 = -4,5
f(0) = 3/2
дальше строим график, если руками - то считаем точки и соединяем плавной кривой.
примерно представив график можно проверить нули функции:
f(-1) = 0
f(1/2) = 0
f(3) = 0
Пошаговое объяснение:
1) x²+y²-10*x+9=(x²-10*x)+y²+9=[(x-5)²-25]+y²+9=(x-5)²+y²-16=0, откуда (x-5)²+y²=16=4² - это уравнение окружности с центром в точке O(5;0) и радиуса R=4.
2) Уравнение эллипса имеет вид x²/a²+y²/b²=1, где a и b - большая и малая полуоси эллипса. Фокусное расстояние эллипса c=[7-(-7)]/2=7. Так как b²=a²-c² и e=c/a, то a=c/e=7/0,28=25 и тогда b=√(a²-c²)=√576=24. Поэтому уравнение эллипса таково: x²/625+y²/576+1.
3) Уравнение параболы задано в форме y²=2*p*x, откуда p=8/2=4 - расстояние от фокуса до директрисы параболы. Поэтому директриса имеет уравнение x=-p/2=-2, а абсцисса фокуса x0=x+p=x+4=2. Поэтому фокус имеет координаты (2;0.