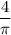Войти Регистрация Спроси ai-bota

Без Лопиталя как решать?

Без Лопиталя как решать?

Показать ответ

Ответ:

nataprada

22.11.2020 17:11

$\displaystyle \lim_{x \to 1}(1-x^{2})\,\text{tg}\, \frac{\pi x}{2} = [0 \cdot \infty] = \lim_{x \to 1}(1-x^{2})\dfrac{\sin \dfrac{\pi x}{2} }{\cos \dfrac{\pi x}{2} } =$

$\displaystyle = \underset{1}{\underbrace{\lim_{x \to 1} \sin \dfrac{\pi x}{2}}} \cdot \lim_{x \to 1}\frac{1 - x^{2}}{\cos \dfrac{\pi x}{2} } = \lim_{x \to 1}\frac{1 - x^{2}}{\cos \dfrac{\pi x}{2} } = \left[\frac{0}{0} \right] =$

$\displaystyle = \left|\begin{array}{ccc}x = 1 - t\\t = 1 - x\\t \to 0\end{array}\right| = \lim_{t \to 0} \frac{1 - (1 - t)^{2}}{\cos \dfrac{\pi(1-t)}{2} } = \lim_{t \to 0} \frac{t(2-t)}{\cos\left(\dfrac{\pi}{2} - \dfrac{\pi t}{2} \right)} =$

$= \displaystyle \lim_{t \to 0}\frac{t(2-t)}{\sin \dfrac{\pi t}{2} } = \left | {{\sin \dfrac{\pi t}{2} \sim \dfrac{\pi t}{2} } \atop {t \to 0}} \right | = \lim _{t \to 0} \frac{t(2-t)}{\dfrac{\pi t}{2} } = \lim_{t \to 0} \frac{4 - 2t}{\pi} =\frac{4}{\pi}$

ответ: $\dfrac{4}{\pi}$

0,0(0 оценок)

Популярные вопросы: Математика

Spale4ik

13.05.2023 02:31

Разложите на множители...

Алимакдр

15.07.2022 08:06

За 3 часа автотурист проехал 211,5 км.какое расстояние он преодолеет за 5 часов, если будет двигаться с той же скоростью...

AnToNoVa13

15.07.2022 08:06

Длина прямоугольника 1 целая 4/20м,а ширина на 3/20меньше длины. найди периметр прямоугольника и вырази его в сантиметрах....

Milena200516

15.07.2022 08:06

Величина которая измеряется в литрах 11 букв...

Profesor245

15.07.2022 08:06

Найди диаметр круга,если его площадь равна 78,12 (п 3,14)...

таня2024

15.07.2022 08:06

Удівчинки було дві монети по 5 к. вона купила стержень для ручки за 8 к. скільки копійок здачі одержала дівчинка?...

Kattemrrr

15.07.2022 08:06

Из 112 кг.железной руды получают 84кг железа.сколько килограммов железа можно получить из 64кг.руды?...

Kerisha4

22.05.2021 14:25

Плоскости α и β, расстояния между которыми 8см, параллельны. ,прямая с лежит в плоскости β. чему равно расстояния от прямой с до плоскости β....

Love25252525

22.05.2021 14:25

Придумайте пять дробей,у которых числитель на 3 меньше знаменателя.запишите пять дробей,у которых числитель в три раза больше знаменателя....

Лизок892

22.05.2021 14:25

1)запиши ряд чисел, в котором первым будет число 23, вторым 46, а каждое следующее число равно сумме двух предыдущих. продолжай ряд, пока будут получатся трехзначные...

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку