Автомобіль виїхав із А в В.За першу годину він проїхав 1,3 всього шляху,за другу-40% решти,а за третю-0,6 нової решти,а за четверту-останні 72км.Знайти відстань між ними А та В.
Решение. Убедимся, что точка не лежит на прямой, данной в условии:
4/5 ≠ (3-1)/-1 ≠ (1+3)/3.
Из уравнения данной прямой следует, что точка M1(0;1; -3) лежит на этой прямой.
Пусть M(x;y;z) - произвольная точка искомой плоскости, тогда векторы MoM(x-4; y-3; z-1), M1Mo(4; 2; 4) и s(5; -1; 3) компланарны. Следовательно, их смешанное произведение равно нулю:
1) х : 5 = 21 : 15 3) 4,5 : 0,6 = х : 2,4
х · 15 = 5 · 21 0,6 · х = 4,5 · 2,4
х · 15 = 105 0,6 · х = 10,8
х = 105 : 15 х = 10,8 : 0,6
х = 7 х = 18
2) 12/х = 8/18 4) (3,4)/(5,1) = (1,4)/х
х · 8 = 12 · 18 3,4 · х = 5,1 · 1,4
х · 8 = 216 3,4 · х = 7,14
х = 216 : 8 х = 7,14 : 3,4
х = 27 х = 2,1
Провести плоскость через прямую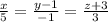
и точку Mo(4; 3; 1).
Решение. Убедимся, что точка не лежит на прямой, данной в условии:
4/5 ≠ (3-1)/-1 ≠ (1+3)/3.
Из уравнения данной прямой следует, что точка M1(0;1; -3) лежит на этой прямой.
Пусть M(x;y;z) - произвольная точка искомой плоскости, тогда векторы MoM(x-4; y-3; z-1), M1Mo(4; 2; 4) и s(5; -1; 3) компланарны. Следовательно, их смешанное произведение равно нулю:
x-4 y-3 z-1| x-4 y-3
4 2 4| 4 2
5 -1 3| 5 -1 =
= 6(x-4) + 20(y-3) - 4(z-1) - 12(y-3) + 4(x-4) - 10(z-1) =
= 6x -24 +20y - 60 - 4z + 4 - 12y + 36 + 4x - 16 - 10z + 10 =
= 10x + 8y - 14z - 50 = 0 или, сократив на 2:
5x + 4y - 7z - 25 = 0.
Таким образом, нормальный вектор искомой плоскости равен:
(5; 4; -7).