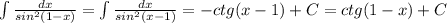Следует применять подстановку так, что бы полностью избавиться от знака радикала. Поскольку в знаменателе присутствует 3 и 4 степень то применяем подстановку 2) = 2x - 1; x = (t¹² +1)/2; dx = 6t¹¹
Теперь нужно сделать обратную подстановку
11. Укажите соответствие между функциями и их неопределенными интегралами
1. т.к. треуг. прямоугольный, то гипотенуза - диаметр, а половина гипотенузы - радиус. Найдем гипотенузу по т. Пифагора:
Получается, радиус будет равен 10÷2=5 см.
ответ: 5 см.
2. Все углы четырехугольника вписанные, т.е. равны половине дуги, на которую они опираются.
Дуга АD= дугаАС-дуга CD=180-60=120 градусов.
Дуга АВ=дугаАС-дуга ВС=180-100=80 градусов.
УголАВС=CDA=180/2=90 градусов (т.к. эти углы опираются на диаметр);
угол ВАD=(дугаВС+дугаCD)/2=(100+60)/2 =160/2=80 градусов.
УголВСД=(дугаАВ+дугаAD)/2=(80+120)/2=200/2=100 градусов.
ответ: 90 градусов, 90 градусов, 80 градусов, 100 градусов.
ответ: t¹² = 2x - 1
11. 1)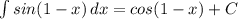
2)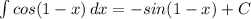
3)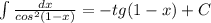
4)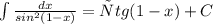
Пошаговое объяснение:
10. В неопределенном интеграле![\int\limits{\frac{\sqrt{2x-1} }{\sqrt[3]{2x-1} +\sqrt[4]{2x-1} } } \, dx](/tpl/images/0132/5542/a0680.png) следует применить подстановку
следует применить подстановку
1) t⁴ = 2x - 1; 2) t¹² = 2x - 1; 3) t³ = 2x - 1; 4) t² = 2x - 1;
Следует применять подстановку так, что бы полностью избавиться от знака радикала. Поскольку в знаменателе присутствует 3 и 4 степень то применяем подстановку 2) = 2x - 1; x = (t¹² +1)/2; dx = 6t¹¹
Теперь нужно сделать обратную подстановку![t=\sqrt[12]{2x-1}](/tpl/images/0132/5542/36e63.png)
11. Укажите соответствие между функциями и их неопределенными интегралами
1.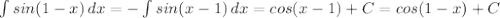
Проверка:(cos(1-x))' = -sin(1 - x)*(1 - x)' = sin(1 - x)
2.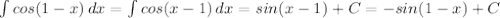
3.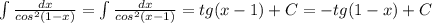
4.