6. Довжина кола дорівнює 14π см. Знайдіть периметр прямокутника, більша сторона якого дорівнює потроєному радіусу даного кола, а менша сторона -- на 45 % більша за діаметр Цього кола.
Пусть - это сторона, равная 9 см, - сторона, равная 10 см, - сторона, равная 11 см. Напротив большей стороны лежит больший угол, следовательно, самый большой угол в этом треугольнике, тот, что лежит напротив .
По теореме косинусов:
- искомая величина. Выражаем её и вычисляем:
Так как самый большой угол данного треугольника имеет положительный косинус, то этот треугольник остроугольный (косинус прямого угла равен нулю, а тупого - отрицателен. Так как у нас косинус самого большого угла в треугольнике положителен, то этот угол является острым).
Пусть а - это длина меньшего осн, b - длина большего основания трапеции. с - длина боковых сторон. h - высота. S=(1/2)*(a+b)*h.
так как окружность вписана в трапецию, то h=2r=4 и a+b=2c.
(В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противолежащих сторон равны. Отсюда следует, что если в трапецию вписана окружность, то сумма ее оснований равна сумме боковых сторон.)
S=(1/2)*(2c)*h=c*h по правилу прямоугольного треугольника с(гипотинуза)=h(высота)/sin30=h/(1/2)=2h
Пусть - это сторона, равная 9 см,
- это сторона, равная 9 см, 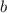 - сторона, равная 10 см,
- сторона, равная 10 см,  - сторона, равная 11 см. Напротив большей стороны лежит больший угол, следовательно, самый большой угол в этом треугольнике, тот, что лежит напротив
- сторона, равная 11 см. Напротив большей стороны лежит больший угол, следовательно, самый большой угол в этом треугольнике, тот, что лежит напротив  .
.
По теореме косинусов:
Так как самый большой угол данного треугольника имеет положительный косинус, то этот треугольник остроугольный (косинус прямого угла равен нулю, а тупого - отрицателен. Так как у нас косинус самого большого угла в треугольнике положителен, то этот угол является острым).
так как окружность вписана в трапецию, то h=2r=4 и a+b=2c.
(В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противолежащих сторон равны. Отсюда следует, что если в трапецию вписана окружность, то сумма ее оснований равна сумме боковых сторон.)
S=(1/2)*(2c)*h=c*h по правилу прямоугольного треугольника с(гипотинуза)=h(высота)/sin30=h/(1/2)=2h
S=ch=2*h*h=2*4*4=32.