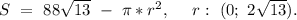по теореме Пифагора квадрат длины диагонали грани равен сумме квадратов длин сторон грани
квадрат длины диагонали прямоугольного паралалепипеда равен сумме квадратов его измерений
пусть а,b,c - его измерения (длині, ширина, высота),d - диагональ первой грани, диагональ второй грани, диагональ третьей грани, диагональ прямоугольного паралелепипеда соотвественно, тогда
Тогда, вырезав из трапеции круг радиуса r, получим фигуру, площадью:
S = s - пr^2 = 88кор13 - пr^2. Каким может быть r?
Проверим можно ли в данную трапецию вписать окружность:
Если в 4-ник можно вписать окружность, то у него суммы противоположных сторон равны.
31+13 = 44
17+17 = 34.
Суммы не равны. Значит окружность, касающуюся всех сторон трапеции вырезать не удастся. Поэтому максимально возможное значение радиуса вырезаемой окружности равно половине высоты:
по теореме Пифагора квадрат длины диагонали грани равен сумме квадратов длин сторон грани
квадрат длины диагонали прямоугольного паралалепипеда равен сумме квадратов его измерений
пусть а,b,c - его измерения (длині, ширина, высота),d - диагональ первой грани, диагональ второй грани, диагональ третьей грани, диагональ прямоугольного паралелепипеда соотвественно, тогда
a^2+b^2=11^2=121
a^2+c^2=19^2=361
b^2+c^2=20^2=400
d^2=a^2+b^2+c^2=1/2((a^2+b^2)+(a^2+c^2)+(b^2+c^2))=1/2 *(121+361+400)=441
d=21 см
ответ: 21 см
ABCD - равноб. трапеция. АD = 31, BC = 13, AB=CD = 17. Проведем высоты: ВК и СМ.
Тогда из равенства тр-ов АВК и СМD следует, что АК = MD = (31-13)/2 = 9.
Найдем высоту из пр. тр. АВК по теореме Пифагора:
ВК = кор(AB^2-AK^2) = кор(289-81) = кор208 = 4кор13.
Найдем площадь трапеции:
s = (31+13)*(4кор13)/2 = 88кор13.
Тогда, вырезав из трапеции круг радиуса r, получим фигуру, площадью:
S = s - пr^2 = 88кор13 - пr^2. Каким может быть r?
Проверим можно ли в данную трапецию вписать окружность:
Если в 4-ник можно вписать окружность, то у него суммы противоположных сторон равны.
31+13 = 44
17+17 = 34.
Суммы не равны. Значит окружность, касающуюся всех сторон трапеции вырезать не удастся. Поэтому максимально возможное значение радиуса вырезаемой окружности равно половине высоты:
r(max) = BK/2 = 2кор13.
Итак, ответ: