1. Все металлы делятся на чёрные, цветные, драгоценные 2. Свойство воспринимать воздействие не разрушаясь - прочность 3.Чугун сплав железа с углеродом более 2% углерода 4. Сталь сплав железа с углеродом, менее 2% углерода 5. По химическому составу стали бывают углеродистые и легированные 6. В зависимости от назначения - конструкционные и инструментальные 7. Свойства углеродистой стали зависят от содержания легирующих элементов и примесей 8. Цветные металлы - медь, алюминий, олово, цинк, серебро 9. Сплавы металлов получают путем смешивания одного металла с другими или металла с неметаллическими элементами. 10. Цели получения сплавов - получение материалов с нужными свойствами
В соответствии с этим строим точки для 16.1. (Картинка 1)
Комплексно-сопряженные числа — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине противоположными по знаку мнимыми частями.
Т.е. сопряженным для числа будет являться число .
В графическом представлении это означает, что сопряженное число будет являться отражением исходного числа относительно действительной оси (оси ).
На Картинке 2 серым обозначены исходные точки и синим - комплексно-сопряженные с ними.
2. Свойство воспринимать воздействие не разрушаясь - прочность
3.Чугун сплав железа с углеродом более 2% углерода
4. Сталь сплав железа с углеродом, менее 2% углерода
5. По химическому составу стали бывают углеродистые и легированные
6. В зависимости от назначения - конструкционные и инструментальные
7. Свойства углеродистой стали зависят от содержания легирующих элементов и примесей
8. Цветные металлы - медь, алюминий, олово, цинк, серебро
9. Сплавы металлов получают путем смешивания одного металла с другими или металла с неметаллическими элементами.
10. Цели получения сплавов - получение материалов с нужными свойствами
Пошаговое объяснение:
Точка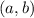
на комплексной плоскости изображает число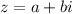 
В соответствии с этим строим точки для 16.1. (Картинка 1)
Комплексно-сопряженные числа — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине противоположными по знаку мнимыми частями.
Т.е. сопряженным для числа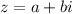
будет являться число 
.
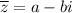В графическом представлении это означает, что сопряженное число будет являться отражением исходного числа относительно действительной оси (оси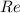
).
На Картинке 2 серым обозначены исходные точки и синим - комплексно-сопряженные с ними.