стройй прямой угол и у тебя получится две стороны, на них откладываешь одинаковые отрезки. и у тебя получится две точки пересечения с прямыми, соединяешь их. Это будет прямоугольный равнобедренный треугольник.
т.к прямой угол равен 90 градусов, то на остальные два приходится тоже 90 градусов.
т. к треугольник равнобедренный то эти два угла равны, значит острый угол такого треугольника равен 45 градусам.
Надеюсь, что Если не сложно и я вам деюйствительно отметьте решение, как лучшее)
Решением неравенства 48 - 13х - х² ≥ 0 есть множество чисел [-16;3] , в котором содержится 20 целых чисел.
а) из этих двадцати чисел только 3 удовлетворяют неравенству х²>0 (1, 2 и 3), значит вероятность будет равна 3/20
б) решением неравенства х² + 10х ≤ 0 есть множество чисел [-10;0] , в котором содержится 11 целых чисел. Все они попадают во множество [-16;3] . Вероятность равна 11/20
в) решением неравенства х² < 101 есть множество чисел , в котором содержится 21 целое число, из которых 14 попадают во множество [-16;3] (числа от -10 до 3) . Вероятность равна 14/20 = 7/10
г) решением неравенства 4х² - 20х + 21 < 0 есть множество чисел (1,5; 3,5) , в котором содержится 2 целых числа (2 и3), оба попадают во множество [-16;3]. Вероятность равна 2/20 = 1/10
я рисунок прислать не могу(
стройй прямой угол и у тебя получится две стороны, на них откладываешь одинаковые отрезки. и у тебя получится две точки пересечения с прямыми, соединяешь их. Это будет прямоугольный равнобедренный треугольник.
т.к прямой угол равен 90 градусов, то на остальные два приходится тоже 90 градусов.
т. к треугольник равнобедренный то эти два угла равны, значит острый угол такого треугольника равен 45 градусам.
Надеюсь, что Если не сложно и я вам деюйствительно отметьте решение, как лучшее)
Решением неравенства 48 - 13х - х² ≥ 0 есть множество чисел [-16;3] , в котором содержится 20 целых чисел.
а) из этих двадцати чисел только 3 удовлетворяют неравенству х²>0 (1, 2 и 3), значит вероятность будет равна 3/20
б) решением неравенства х² + 10х ≤ 0 есть множество чисел [-10;0] , в котором содержится 11 целых чисел. Все они попадают во множество [-16;3] . Вероятность равна 11/20
в) решением неравенства х² < 101 есть множество чисел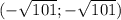 , в котором содержится 21 целое число, из которых 14 попадают во множество [-16;3] (числа от -10 до 3) . Вероятность равна 14/20 = 7/10
, в котором содержится 21 целое число, из которых 14 попадают во множество [-16;3] (числа от -10 до 3) . Вероятность равна 14/20 = 7/10
г) решением неравенства 4х² - 20х + 21 < 0 есть множество чисел (1,5; 3,5) , в котором содержится 2 целых числа (2 и3), оба попадают во множество [-16;3]. Вероятность равна 2/20 = 1/10