348. определите диаметр и радиус окружности,
если ее длина равна:
а) 314 см; г) 47,1 см;
ж) 355/113
б) 15,7 м;
д) 4.
920
м;
дм;
b) 18,84 дм;
и) 286 мм.

Показать ответ

Ответ:

revunova

23.04.2021 07:41

Решение:

Сначала найдем производную функции:

$\displaystyle \Big ( y \Big )' = \Big ( (x^2-39x+39) \cdot e^{2-x} \Big ) ' = \\\\\\= \Big ( x^2-39x+39 \Big ) ' \cdot e^{2-x} + \Big (e^{2-x} \Big ) ' \cdot (x^2-39x+39) = \\\\\\= \Big ( 2x - 39 \Big ) \cdot e^{2-x} +\Big ( (-1) \cdot e^{2-x} \Big ) \cdot (x^2 - 39x + 39) = \\\\\\= e^{2-x} \cdot \Big ( (2x-39)-(x^2-39x+39) \Big ) = \\\\\\= e^{2-x} \cdot (-x^2 + 41x - 78)$

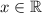Также заметим, что функция, как и производная, определена для всех значений (иначе говоря, $x \in \mathbb R$ ). Теперь, чтобы найти критические точки производной, приравняем ее к нолю:

$e^{2-x} \cdot (-x^2 + 41x - 78) = 0$

Сразу же заметим, что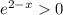 $e^{2-x} 0$ , поэтому обе части можно разделить на данное выражение:

$-x^2 + 41x - 78 = 0 \;\;\; \Big | \cdot (-1) \\\\x^2 - 41x + 78 = 0$

Дальше воспользуемся теоремой Виета:

$\displaystyle \left \{ {{x_1+x_2=41} \atop {x_1 \cdot x_2=78}} \right. ; \;\;\; \Rightarrow \;\;\; \left \{ {{x_1=2} \atop {x_2=39}} \right.$

Полученные две точки выставим на координатной прямой, а потом на получившихся трех промежутках расставим знаки производной:

- - - + + + - - -

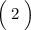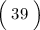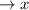
________ $\Big ( \; 2 \; \Big )$ ________ $\Big ( \; 39 \; \Big )$ ________ $\rightarrow x$

Можно сделать вывод, что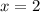 x=2 - точка минимума функции (в силу того, что знак меняется с «-» на «+»), а 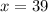x=39 - точка максимума (так как происходит смена знака с «+» на «-»).

Дальше остается заметить, что единственная точка минимума функции (как мы ранее получили,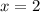 x=2 ) располагается на заданном в условии отрезке $\Big [ 0; 6 \Big ]$ .

Эта точка также будет соответствовать ответу, так как на промежутке [0;2] функция убывает, а на промежутке [2;6] - возрастает:

↘ ↗

$\Big ( \; 0 \; \Big )$ _______ $\Big ( \; 2 \; \Big )$ _______ $\Big ( \; 6 \; \Big )$

Точку, соответствующую ответу, мы нашли. Осталось только определить значение функции в этой точке:

$y(2) = (2^2-39 \cdot 2+39) \cdot e^{2-2} = (4 - 39) \cdot 1 = \underbrace { \; -35 \; } _{\text{min} \;y}$

Задача решена!

ответ: - 35 .
Найдите наименьшее значение функции y=(x^2-39x+39)*e^(2-x) на отрезке [ 0; 6]. зарание .

0,0(0 оценок)

Ответ:

nikolottorres

24.10.2020 15:39

1)Dort ist der Bleistift,den ich brauche.
2) Vorn sitzt der Schüler,dem diese Schultasche gehört.
3) Ich wähle das Buch,dessen Autor mir bekannt ist.
4) Die Schülerin,die an der Tafel steht, besucht diesen Zirkel.
5) Das sind die Kinder,deren Bücher hier liegen.
6) Das ist ein Mädchen,das mit der Puppe spielt.
7) Das Mädchen,dessen Mutter ich gut kenne, ist eine fleißige Schülerin.
8) In diesem schönen Haus,das ein großes Museum ist, ist ein bekannter Dichter geboren.
9) Neben mir sitzt ein Junge,dem ich über dieses Buch erzählte.
10) Die Lehrerin ruft die Kinder,deren Schulsachen hier liegen.
11) Der Schriftsteller,dessen Roman wir gelesen habem, ist weltberühmt.
12) Das ist die Blume,die ich gepflanzt habe.

0,0(0 оценок)

Популярные вопросы: Математика