3. в городе имеется 5 оптовых баз. вероятность того, что товар требуемого сорта отсутствует на этих базах, одинакова и равна 0.3. составить закон распределения случайной величины x-числа баз, на которых искомый товар отсутствует в данный момент. найти ожидание и среднее квадратическое отклонение
а) Пестрик; b) Черныш; с) Пестрик; d) Пестрик
Пошаговое объяснение:
Исходя из этих данных, можно составить в каждом случае уравнение и по нему определить кто взял последним.
Формула нашего уравнения будет следующая:
х=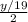
y - Это количество початков.
первым по порядку у нас идет Пестрик, если он взял последние 19 початков число будет с дробью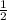
и больше, если число будет цельным, либо с другой дробью которая меньше 
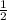, значит последние 19 початков за Чернышом.
а) х=(323/19)/2
х=17/2
х=8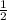
(Пестрик)
б) х=(621/19)/2
х=621/38
х=16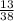
(Черныш)
с) х=(455/19)/2
х=455/38
х=11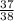
(Пестрик)
d) х=(400/19)/2
х=400/38
х=10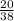
(Пестрик)
Для построения графика \left|x\right| + \left|y\right| = 1∣x∣+∣y∣=1 воспользуемся определением модуля числа:
\begin{lgathered}\left|a\right| = \begin{cases} a, & a \geqslant 0 \\ -a & a < 0\end{cases}\end{lgathered}
∣a∣={
a,
−a
a⩾0
a<0
Вся координатная плоскость состоит из четырёх квадрантов, в каждом из которых знак xx и yy остаётся постоянным, поэтому в каждом квадранте можно избавиться от модулей и построить соответствующие фрагменты графика \left|x\right| + \left|y\right| = 1∣x∣+∣y∣=1 .
1. Пусть x > 0x>0 и y > 0y>0 , тогда \left|x\right| + \left|y\right| = x + y = 1∣x∣+∣y∣=x+y=1 , поэтому в I-й четверти строим график функции y = 1 - xy=1−x .
2. Пусть x < 0x<0 и y > 0y>0 , тогда \left|x\right| + \left|y\right| = -x + y = 1∣x∣+∣y∣=−x+y=1 , поэтому во II-й четверти строим график функции y = 1 + xy=1+x .
3. Пусть x < 0x<0 и y < 0y<0 , тогда \left|x\right| + \left|y\right| = -x - y = 1∣x∣+∣y∣=−x−y=1 , поэтому в III-й четверти строим график функции y = -1 - xy=−1−x .
4. Пусть x > 0x>0 и y < 0y<0 , тогда \left|x\right| + \left|y\right| = x - y = 1∣x∣+∣y∣=x−y=1 , поэтому в IV-й четверти строим график функции y = x - 1y=x−1 .
График с пояснениями и этапами построения приведён на прилагаемом рисунке.