2sin(п+a)sin(п/2+a)-sin2a​

х = 6

х = 6у = 3

Пошаговое объяснение:

17x-30y=12

17x-30y=12-5x+6y=-12

17x-30y=12-5x+6y=-1217x-30y=12

17x-30y=12-5x+6y=-1217x-30y=125х - 6у = 12

17x-30y=12-5x+6y=-1217x-30y=125х - 6у = 1217х - 30у = 5х - 6у

17x-30y=12-5x+6y=-1217x-30y=125х - 6у = 1217х - 30у = 5х - 6у12х = 24у

17x-30y=12-5x+6y=-1217x-30y=125х - 6у = 1217х - 30у = 5х - 6у12х = 24ух = 2у

Отсюда:

Отсюда:17x-30y = 34у - 30у

Отсюда:17x-30y = 34у - 30у34у - 30у = 12

Отсюда:17x-30y = 34у - 30у34у - 30у = 124у = 12

Отсюда:17x-30y = 34у - 30у34у - 30у = 124у = 12у = 3

Отсюда:17x-30y = 34у - 30у34у - 30у = 124у = 12у = 3х = 2у

Отсюда:17x-30y = 34у - 30у34у - 30у = 124у = 12у = 3х = 2уЗначит

Отсюда:17x-30y = 34у - 30у34у - 30у = 124у = 12у = 3х = 2уЗначит х = 6

SΔABC = 3 *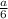 AD = 3Q

Пошаговое объяснение:

1) Рассмотрим ΔCMB:

Scmb = Samc (т.к. основание - равносторонний треугольник, то MA = MC = MB ⇒ площади граней равны) = Q

Scmb =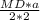 = = 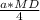Q (a - сторона ΔABC)

2) Рассмотрим ΔOMD:

Так как ∠ODM = 60°, то ∠OMD = 30° ⇒ OD =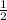 MD (сторона, лежащая против угла 30° равна половине гипотенузы)

3) Так как ΔABC равносторонний, то все высоты пересекаются в одной точке и делятся ей в отношении 1:2 (OD =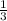 AD)

4) SΔ =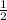   a * h ⇒ SΔABC = 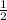a * AD

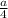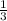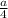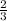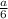Q = * MD; MD = 2*OD; OD = AD ⇒ Q = * AD = AD

SΔABC = 3 *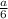 AD = 3Q