2 задачи на теорию вероятности. 1.В группе имеется 19 студентов, среди которых 3 – отличника. По списку наудачу отобрано 5 студентов.
Найти вероятность того, что среди отобранных студентов не более 3 отличников.
2.В ящике находятся 13 деталей, из которых окрашено 4. Сборщик наудачу взял три детали. Найти вероятность того, что будут окрашены не более двух деталей.
Заранее очень благодарен.
1) 1; 2) 141/143
Пошаговое объяснение:
1) Вероятность того, что среди отобранных студентов будет больше 3 отличников равна нулю, так как в классе всего 3 отличника. Тогда вероятность не более трёх отличников равна 1.
2) Необходимо найти вероятность того, что среди взятых наудачу 3 деталей либо 2, либо 1, либо 0 будут окрашенными.
Посчитаем число комбинаций с подобным исходом.
Комбинации, при которых взято 2 из 4 окрашенных и 1 из 9 неокрашенных деталей: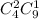
Комбинации, при которых взято 1 из 4 окрашенных и 2 из 9 неокрашенных детали: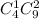
Комбинации, при которых взято 0 из 4 окрашенных и 3 из 9 неокрашенных детали: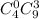
Получаем, что суммарное число комбинаций, удовлетворяющих нашему условию: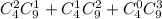
Теперь посчитаем число комбинаций при взятии 3 случайных деталей, вне зависимости от их окраски: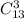
Тогда вероятность получить не более 2 окрашенных деталей: