2 вариант 1 задание:

Найдите соответствие между рисунком, числовым промежутком и неравенством: Изображение на координатной Обозначение неравенство

прямой

1.

2

А) (- о 0; 4)

B)[-2; 00)

C)(-2; 4)

D) (4; 0)

E) –2; 4)

F) (-2; 9)

1) -2 <x<4

2) х > 4

3) x2-2

4)-2<x<4

5) х<4

6) x2-2

II.

х

II.

Показать ответ

Ответ:

vkovbasa99

14.11.2020 17:57

138π см²

Пошаговое объяснение:

Построим равнобедренную трапецию ABCD с высотой CF (см. Рис. 1).

Согласно условию: AD=18 см, BC=10 см, CF=3 см. Для дальнейших вычислений нам понадобится длина боковой стороны трапеции AB=CD.

Т.к. трапеция равнобедренная, то FD = (AD-BC):2 = 4 см.

ΔCDF - прямоугольный с катетами CF=3 см, FD=4 см, значит он египетский, и его гипотенуза CD=5 см.

При вращении такой трапеции вокруг короткого основания образуется цилиндр с равными осевыми конусообразными выемками с обеих сторон (См. рис. 1.2, 2.1, 2.2). Радиус такого цилиндра равен высоте трапеции R=CF=3 см, а высота цилиндра равна длинному основанию трапеции H=AD=18 см.

Образующей конуса-выемки является боковая сторона трапеции L=CD=5 см, радиус равен радиусу цилиндра R=3 см.

Искомая площадь полной поверхности фигуры вращения состоит из площади боковой поверхности цилиндра и двух боковых поверхностей конусов-выемок.

Площадь боковой поверхности цилиндра: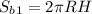 $S_b_1=2\pi RH$ .

Площадь боковой поверхности конуса-выемки: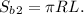 $S_b_2=\pi RL.$

Площадь полной поверхности: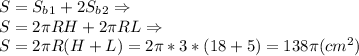 $S=S_b_1 +2S_b_2 \Rightarrow\\S=2\pi RH+2\pi RL \Rightarrow\\S=2\pi R(H+L) = 2\pi *3*(18+5)=138\pi (cm^2)$

Равнобедренная трапеция с основаниями 10 см и 18 см и высотой 3 см вращается около меньшего основани

0,0(0 оценок)

Ответ:

Anya18121978

28.05.2021 09:30

В правильной четырехугольной призме площадь основания равна 10, а боковое ребро 3√10. Найдите расстояние между стороной основания и диагональю призмы, не пересекающейся с ней.

––––––––––––––––––––––––––––

На рисунке, данном в приложении, сторона основания и диагональ призмы, не пересекающаяся с ней – прямые АД и А1С. Они скрещивающиеся.

Определение: Расстояние между скрещивающимися прямыми – это расстояние между одной из скрещивающихся прямых и параллельной ей плоскостью, проходящей через другую прямую.

Через диагональ призмы А1С и сторону ВС проведем плоскость ВСД1А1. Плоскость содержит ВС║ АД, значит, она параллельна АД ( по т. о параллельности прямой и плоскости).

Длина перпендикуляра, опущенного на эту плоскость из любой точки на прямой АД – есть искомое расстояние.

Отметим на АД точку М.

Проведем отрезок МК║ДД1 и отрезок МН║ ДС. Они будут взаимно перпендикулярны. Соединив К и Н, получим прямоугольный треугольник КМН, в котором гипотенуза КН лежит в плоскости ВА1Д1Д. Следовательно, высота МО этого треугольника – расстояние между АД и плоскостью, содержащей диагональ призмы.

По т.Пифагора найдем КН.

КН=СД1, МН=ДС, КМ=ДД1

КН=√(KM²+MH²)=√190

S ∆ CДД1=СД•ДД1:2=10√10):2

S ∆ CДД1=МО•КН:2

МО=2 S ∆СДД1:КН=10√10):√190=10/√19 - искомое расстояние.

Тот же результат получим, если из прямого угла Д грани ДСС1Д1 опустим перпендикуляр на СД1 или из А – на ВА1, т.к., если прямая параллельна плоскости, то все точки этой прямой равноудалены от той плоскости.