2. В треугольнике ABC BC = ВА =10, AC = 8. Пусть АА1 и CC1 биссектрисы треугольника. Найдите отрезок А1C1​

Примем за икс массу масла в первом сосуде.

Тогда, как сказано из условия, масса масла во втором сосуде составляет 35% массы масла первого сосуда: 0,35x.

В третьем сосуде масла 5/7 от массы масла второго сосуда:

(5/7)*0,35x;;

Всего масла 32 л.

Составим уравнение:

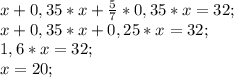
Получили, что в первом сосуде 20 л. масла.

Во втором сосуде, получаем: 0,35*20=7 л.

В третьем сосуде, получаем: (5/7)*7=5 л.

Если сложить массу масла во всех трех сосудах, получим 32 л. Значит, мы все сделали верно.

ответ: В первом сосуде 20 л. масла, во втором сосуде 7 л. масла, в третьем сосуде 5 л. масла.

Пусть событие F - произошло одно попадение в цель. 
Обозначим соссособытия: 
А1- оба охотника не попали в цель 
А2- оба охотника попали в цель 
А3- 1й охотник попал в цель, 2й нет 
А4- 2й охотник попал в цель, 1й нет 

В нашем случае надо будет найти как раз вероятность А4. 

Найдем вероятности гипотез и условные вероятности события F  для этих гипотез: 

P(А1)= 0,8*0,4=0,32          Р_a1 (F) = 0 
Р(А2)=0,2*0,6=0,12           Р_a2 (F) = 0 
Р(А3)=0,2*0,4=0,08           Р_a3 (F) = 1 
Р(А4)=0,6*0,8=0,48           Р_a4 (F) = 1 

Теперь по формуле Байеса: 
Р_f (А4) = (0,48*1) / (0,32*0 + 0,12*0 + 0,08*1 + 0,48*1) = ~ 0.857