Предположим, что такое разбиение возможно и оно выполнено. Обозначим меньшие числа в парах буквами a с индексами:
Индекс совпадает с разностью чисел в паре, в которой состоит соответствующее число.
Тогда большее число в -той паре будет равно , а их (бОльших чисел) последовательность выглядеть так:
Вычислим сумму чисел от 1 до 2020 двумя . С одной стороны, ее можно найти как сумму первых 2020 элементов арифметической прогрессии с первым элементом и разностью :
С другой стороны, можно сложить суммы в парах чисел, используя введенные буквенные обозначения:
Сумму чисел во вторых скобках опять же найдем как сумму первых 1010 элементов арифметической прогрессии с первым элементом и разностью :
Мы подошли к ключевому равенству: приравняем полученные разными путями суммы:
Отсюда
Однако сумма натуральных чисел не может быть дробной! Получили противоречие. А значит, разбиение, о котором идет речь в задаче, невозможно.
Меридианы - это скорее всего медианы. Как известно, медианы треугольника пересекаются в одной точке и в этой точке делятся в отношении 2 к 1, считая от вершины. Поэтому, раз BN=9, то BK=6. Продолжим CK до пересечения с AB в точке L. Поскольку CL медиана, а CK=10, то KL =5. Но треугольник ABK прямоугольный, а KL - медиана прямого угла, поэтому она равна половине гипотенузы AB. Следовательно, AB=10. Зная гипотенузу AB и катет BK, находим второй катет AK по теореме Пифагора (или заметив, что он подобен египетскому треугольнику 3-4-5). Итак, AK=8, а тогда AM=12.
нет
Пошаговое объяснение:
Предположим, что такое разбиение возможно и оно выполнено. Обозначим меньшие числа в парах буквами a с индексами:
Индекс совпадает с разностью чисел в паре, в которой состоит соответствующее число.
Тогда большее число в -той паре будет равно
-той паре будет равно 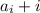 , а их (бОльших чисел) последовательность выглядеть так:
, а их (бОльших чисел) последовательность выглядеть так:
Вычислим сумму чисел от 1 до 2020 двумя . С одной стороны, ее можно найти как сумму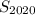 первых 2020 элементов арифметической прогрессии с первым элементом
первых 2020 элементов арифметической прогрессии с первым элементом 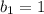 и разностью
и разностью 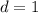 :
:
С другой стороны, можно сложить суммы в парах чисел, используя введенные буквенные обозначения:
Сумму чисел во вторых скобках опять же найдем как сумму первых 1010 элементов арифметической прогрессии с первым элементом
первых 1010 элементов арифметической прогрессии с первым элементом 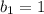 и разностью
и разностью 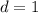 :
:
Мы подошли к ключевому равенству: приравняем полученные разными путями суммы:
Отсюда
Однако сумма натуральных чисел не может быть дробной! Получили противоречие. А значит, разбиение, о котором идет речь в задаче, невозможно.
Меридианы - это скорее всего медианы. Как известно, медианы треугольника пересекаются в одной точке и в этой точке делятся в отношении 2 к 1, считая от вершины. Поэтому, раз BN=9, то BK=6. Продолжим CK до пересечения с AB в точке L. Поскольку CL медиана, а CK=10, то KL =5. Но треугольник ABK прямоугольный, а KL - медиана прямого угла, поэтому она равна половине гипотенузы AB. Следовательно, AB=10. Зная гипотенузу AB и катет BK, находим второй катет AK по теореме Пифагора (или заметив, что он подобен египетскому треугольнику 3-4-5). Итак, AK=8, а тогда AM=12.
ответ: 12