Математика: 12345678-12345678--0 это для 1 класса

12345678-12345678--0 это для 1 класса

Показать ответ

Ответ:

kadalsu4

01.12.2020 23:44

$2 \ln 8 - 4 + \pi.$

Пошаговое объяснение:

Для вычисления интеграла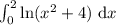 $\int_0^2 \ln (x^2 + 4)\ \text d x$ воспользуемся сначала методом интегрирования по частям:

$u = \ln (x^2 + 4);\ \text d v = \text d x;\\\text d u = \frac{2x}{x^2 + 4}.\ \ \ \ \ \,\,\: x = \int \text d x = x.$

$\int_0^2 \ln (x^2 + 4)\ \text d x = \left \left( x \ln (x^2 + 4) \right) \right | \limits_0^2 - \int_0^2 \frac{2x^2}{x^2+4}\ \text d x.$

Заметим, что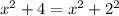 x^2 + 4 = x^2 + 2^2 , и тогда в интеграле после интегрирования по частям напрашивается такая замена:

Если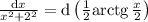 $\frac{\text d x}{x^2 + 2^2} = \text d \left( \frac 12 \text{arctg}\, \frac x2 \right)$ , то, положив 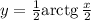$y = \frac 12 \text{arctg}\, \frac x2$ , найдём, что:

$y = \frac 12\, \text{arctg}\, \frac x 2;\\2y = \text{arctg} \frac x 2;\\\text{tg}\, 2y = \frac x 2;\\x = 2\,\text{tg}\, 2y.$

Применим это всё при вычислении получившегося интеграла.

Пределы интегрирования изменятся так:

$a = \frac 12\, \text{tg}\, \frac 0 2 = \frac 12\, \text{tg}\, 0 = 0 \cdot \frac 12 = 0.$

$b = \frac 12\, \text{tg} \frac 2 2 = \frac 12\, \text{tg} \, 1 = \frac 12 \cdot \frac{\pi}{4} = \frac{\pi}{8}.$

Вычислим теперь сам интеграл:

$\int_0^\frac\pi 8 2 \left( 2\, \text{tg}\, 2y \right)^2 \text d y = 8 \int_0^\frac \pi 8 \, \text{tg}^2\, 2y\, \text d y.$

Введём замену: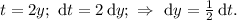 $t = 2y;\ \text d t = 2\, \text d y;\ \Rightarrow\ \text d y = \frac 12\, \text d t.$

Пределы интегрирования изменятся так:

$a = 2 \cdot 0 = 0;\\b = 2 \cdot \frac \pi 8 = \frac \pi 4.$

Продолжим вычисление интеграла:

$4 \int _0^\frac \pi 4\, \text{tg}^2 \, t\, \text d t = 4 \int_0^\frac\pi4 \frac{\sin^2t}{\cos^2t}\, \text d t = 4 \int_0^\frac\pi4 \frac{1 - \cos^2 t}{\cos^2 t} \text d t= 4 \left( \int_0^\frac\pi 4 \frac{\text d t}{\cos^2 t} - \int_0^\frac\pi4\text d t \right) =\\= 4 \left( \text{tg}\, t |_0^\frac\pi4 - t|_0^\frac\pi4 \right) = 4 \left( \text{tg}\, \frac\pi 4 - \text{tg}\, 0 - \frac\pi 4 + 0 \right) = 4 - \pi.$

Подставим найденное значение в выражение после интегрирования по частям и найдём итоговый результат:

$2\ln(2^2 + 4) - 0 \ln (0^2 + 4) - (4 - \pi) = 2 \ln 8 - 4 + \pi.$

Наконец, получаем, что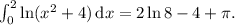 $\int _0^2 \ln (x^2 + 4)\, \text d x = 2 \ln 8 - 4 + \pi.$

0,0(0 оценок)

Ответ:

NastyKot15246

06.04.2022 02:55

Если было поровну рыцарей и лжецов -значит их было четное количество.
Когда первый из 2015 сказал: Когда я уеду, на острове станет поровну рыцарей и лжецов, он мог оказаться рыцарем, т.к. после его уезда оставалось четное кол-во человек (но мог быть и лжецом). Когда уезжал 2 человек и произносил эту фразу -он определенно был лжец, т.к. после его уезда оставалось 2013 человек-т.е. нечетное кол-во. Соответственно, каждый человек, который уезжал четным был лжецом. Выясним сколько их было:
2, 4, 6, , 2014
2014=2+(n-2)2
2012=(n-1)2
n-1=1006
n=1007 -лжецов было точно.
Пройдемся от начала, с новой инфой, что лжецов было ≥1007.

1 случай. Если первый уезжающий -рыцарь, тогда из 2014 поровну рыцарей и лжецов, а также лжецов ≥1007, значит осталось 1007 рыцарей и 1007 лжецов.
Тогда с учетом первого рыцаря на острове было: 1007+1=1008 рыцарей.

2.Случай. Если первый уезжающий -лжец. из 2014 человек лжецов>1007, а рыцарей <1007. Всего лжецов уже >1008 (из 2015 человек)
3ий уезжающий оставил после себя 2012 человек
т.к. лжецов уже >1008, поровну уже ни при каком случае не получится.
(т.к. чтобы из 2012 чел было поровну и л и р, их должно быть по 1006, из 2010 -1005 и меньше,)
Таки образом, последний человек который был 2015 по счету -был рыцарем, так как после него осталось равное кол-во лжецов и рыцарей =0)
итого : 2014 лжецов и 1 рыцарь.

0,0(0 оценок)

Популярные вопросы: Математика