1. вычислите: 1,2: ((−12)^−2 − 2,4^−2) − 2,8.
2. в комнате находятся 80 воздушных шаров — красных и зелёных. известно, что: 1) по крайней мере, один из шаров красный; 2) из каждой произвольно выбранной пары шаров, по крайней мере, один зелёный. сколько в комнате красных шаров?
3. на счет в банк 1 января 2019 года был сделан вклад в 700 рублей под 20% годовой прибыли. через год (после начисления процентов) со счета сняли 440 рублей. найдите сумму, которая будет на счету в банке еще через год (после начисления процентов).
4. найдите произведение целочисленных отрицательных решений неравенства
−(3 + 4)2 < 10 − 3(3 − 6)( + 2)
5. миша играет в интересную компьютерную игру. на каждом следующем уровне он набирает на 6 очков больше, чем на предыдущем. он посчитал, что на первых 10 уровнях он набрал в сумме столько же очков, что и на следующих за ними 5 уровнях. какое количество очков миша набрал на первом уровне?
6. найдите область определения функции () = 6√−22+7−3 √5−5 . в ответе укажите сумму целых значений х из области определения.
7. в треугольнике один из углов в 3 раза больше другого, а разность этих углов 450. найдите медиану, проведенную из вершины третьего угла, если большая сторона треугольника равна 13,5.
8. расстояние между пристанями а и в равно 96 км. из пункта а в пункт в по течению реки отправился плот, а через 1час вслед за ним отправилась яхта, которая, прибыв в пункт в, тотчас повернула обратно и возвратилась в а. к этому времени плот км. найдите скорость яхты в неподвижной воде, если скорость течения реки равна 5 км/ч. ответ дайте в км/ч.
9. найдите все значения параметра p, при которых уравнение
2 + (5 − 2) + 2 − 5 + 4 = 0
имеет 2 корня, один из которых положительный, а другой отрицательный. в ответе укажите количество целых значений параметра р, удовлетворяющих условию.
с пояснением
Пусть сосуд содержал
килограммов раствора до добавления воды. Тогда мы можем составить следующую таблицу:
Кратко поясню ее составление: мы предположили, что "сначала" (то есть до добавления воды) общая масса раствора была равна_______________________________________________
Соли, кг: Всего, кг:
Сначала: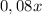
Потом: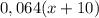
_______________________________________________
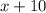Так как количество соли должно было остаться неизменным, то (соль ни откуда не появлялась и никуда не испарялась, только прибавили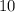
литров несоленой воды):
Значит, до добавления воды ("сначала") сосуд содержал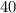
килограммов раствора.
Задача решена!
ответ: 40 килограммов раствора.Даны вершины пирамиды A(3;-2;3)B(-1;0;2)C(-3;1;-1)D(-3;-3;1) .
Находим векторы АВ, АС и АД.
Вектор АВ = (-4; 2; -1 ), модуль равен √(16+4+1) = √21 ≈ 4,58258.
Вектор АC={xC-xA, yC-yA, zC-zA} = (-6; 3; -4) =√61 ≈ 7,81025.
Вектор АD={xD-xA, yD-yA, zD-zA} = (-6; -1; -2) = √41 ≈ 6,40312.
Определяем векторное произведение АВ х АС.
i j k | I j
-4 2 -1 | -4 2
-6 3 -4 | -6 3 = -8i + 6j - 12k - 16j + 3i + 12k = -5i - 10j = (-5; -10; 0).
Далее находим смешанное произведение (АВ х АС) х АД.
(АВ х АС) = (-5; -10; 0),
АD = (-6; -1; -2),
(АВ х АС) х АД = 30 + 10 + 0 = 40.
Объем пирамиды равен (1/6) этого произведения:
V = (1/6)*40 = (20/3) куб.ед.
Высота h пирамиды ABCD, опущенная из вершины D на плоскость основания ABC, равна: h = 3V/S(ABC).
Площадь основания АВС равна половине модуля векторного произведения АВ х АС.
S(ABC) = (1/2)*√((-5)² + (-10)² + 0²) = (1/2)√(25 + 100) = (5/2)√5 кв.ед.
h = (3*20/3)/((5/2)√5) = 8/√5 = 8√5/5 ≈ 3,5777.