1) Основа піраміди — ромб, більша діагональ якого d, а гострий кут 60°. Всі двогранні кути при основі дорівнюють по 60°. Знайдіть площу повної поверхні піраміди. 2) Основа піраміди — квадрат, дві грані перпендикулярні основі піраміди. Дві інші бічні грані піраміди нахилені до основи піраміди під кутом (; висота піраміди Н. Знайдіть площу бічної поверхні піраміди.

Показать ответ

Ответ:

tahogomelp07u2x

25.04.2021 19:33

Пусть размер кредита равен А млн. рублей.

В середине 1-го года долг возрастёт на 25%, то есть увеличиться на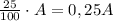 $\frac{25}{100}\cdot A=0,25A$ млн. рублей , и станет равным (А+0,25А)=1,25А млн. руб. (Можно сказать, что сумма долга увеличилась в 1,25 раз и становится равной 1,25А млн.руб.)

В конце 1-го года заёмщик выплачивает только % по кредиту, то есть выплачивает 0,25А млн. руб. Аналогично, в конце 2-го года заёмщик выплачивает 0,25А млн. руб. В сумме за два года погашается сумма в 0,25А+0,25А=0,5А млн.руб.

В середине 3-го года сумма долга сначала возрастает в 1,25 раза, то есть становится равной 1,25А, а в конце этого года выплачивается некоторая сумма, равная Х млн.руб. После выплаты заёмщиком этих Х млн.руб. в конце 3-го года останется долг, равный (1,25А-Х) млн.руб.

В середине 4-го года долг опять увеличиться в 1,25 ( от оставшейся суммы долга) и станет равным 1,25*(1,25А-Х). В конце 4-го года заёмщик должен выплатить Х млн. руб., т.к. он по условию задачи должен в конце 3-го и 4-го годов выплатить равные суммы.И так как это будет последний платёж, то заёмщик уже погасит долг до 0 . Отсюда получаем уравнение:

$1,25\cdot (1,25A-X)-X=0\\\\1,25^2A-1,25X-X=0\; \; \to \; \; \; 1,25^2A=2,25X\\\\X=\frac{1,25^2A}{2,25}$

Теперь найдём общую сумму выплат:

$0,5A+2X=0,5A+2\cdot \frac{1,25^2A}{2,25}=(\frac{1}{2}+\frac{3,125}{2,25})\cdot A=\frac{17}{9}\cdot A$

По условию общая сумма выплат превышает 5 млн.руб., значит

$\frac{17}{9}\cdot A5\; \; \Rightarrow \; \; A\frac{5\cdot 9}{17}\; ,\; \; A\frac{45}{17}\; ,\; \; A2\frac{11}{17}$

Наименьшее целое число, при котором выполняется последнее неравенство - это число 3. Значит, наименьший размер кредита, при котором общая сумма выплат заёмщика превысит 5 млн.руб. , равна 3 млн.руб.

0,0(0 оценок)

Ответ:

kiggiydduii

15.07.2020 10:59

Пусть Т - время, за которое велосипедист проехал гипотенузу. И за это же время он проехал два катета.
Пусть х - длина меньшего катета, х+2 - длина большего катета.
30Т - длина гипотенузы.
42Т - длина суммы двух катетов.
42Т = х+х+2
42T = 2x+2
42T = 2(x+1)
21T = x+1
x = 21T-1 - длина меньшего катета
х+2 = 21Т-1 + 2 = 21Т+1 - длина большего катета.
Квадрат гипотенузы равен сумме квадратов катетов.
(30Т)^2 = (21Т+1)^2 + (21Т-1)^2
900Т^2 = 441Т^2 + 42Т + 1 + 441Т^2 - 42Т + 1
900Т^2 - 882Т^2 - 2 = 0
18Т^2 - 2 = 0
9Т^2 - 1 = 0
(3Т+1)(3Т-1) = 0
Два корня будут решениями этого уравнения:
3Т + 1 = 0
Т = -1/3 - не подходит, так как время не может иметь отрицательное значение.
3Т - 1 = 0
Т = 1/3 - время, за которое велосипедист проехал гипотенузу, пища такое же время проехал два катета.
30Т = 30 • 1/3 = 10 км - длина гипотенузы.
Но х = 21T-1 - длина меньшего катета.
х+2 = 21Т-1 + 2 = 21Т+1 - длина большего катета.
Значит,
1) 21 • 1/3 - 1 = 7-1 = 6 км - длина меньшего катета.
2) 21 • 1/3 + 1 = 7+1 = 8 км - длина большего катета.
3) 10 + 6 + 8 = 24 км - протяженность Асей трассы.
ответ: 24 км.

Проверка.
Проверим, соответствуют ли длины сторон прямоугольного треугольника закону «Квадрат гипотенузы равен сумме квадратов катетов»:
6^2 + 8^2 = 36 + 64 = 100 - сумма квадратов катетов ю.
10^2 = 100 - квадрат гипотенузы.

0,0(0 оценок)

Популярные вопросы: Математика