1.Найдите обратную функцию данной функции : y = (x-3)/2
A) y = 2x +3 B) y = 2x – 3 C)y = x/2 – 3
D) y = (x-3)/2 E) y = (x+3)/2
2. Найдите обратную функцию данной функции: f(x) = ( x – 〖3)〗^(2 )+ 1, x ≥ 3.
A)y = 3 – √(x-1) B) y = 3 ± ( x – 〖1)〗^2
C) y = 3 + √(x-1) D) y = 3 ± √(x-1)
E) y = 3 + ( x – 〖1)〗^2
3. Найдите обратную функцию данной функции: y = x^2, если x < 0
A) y =√x B) y = ± 1/√x C) y = ± √x
D) y = - 1/√x E) y = - √x
4. Дана функция у = -х2 - 4х + 5. Вычислите значения этой функции при х=-2 и х=-6. Запишите сумму получившихся значений.
А) 2; В) 2,5; С) 0,5; D) 1,8 Е) -2
5. Дана функции y=- 6/x . Какая линия является ее графиком?
A) прямая, проходящая через начало координат
В) прямая, не проходящая через начало координат
С) парабола
D) гипербола
Е) полу парабола
6. График функции сдвинули вправо на 2 единицы, а затем вниз на 3 единицы. Запишите полученную функцию.
А) В) С) D) Е)
7.Решите систему уравнений: {█(sin x+cos y= 1/[email protected] y-sin x=1/2)┤
A) ( k π (±〖1)〗^k π/3+kπ) n,k € ℤ
B) ( π/3+nπ;(-〖1)〗^(k ) π/6+2k π) n,k € ℤ
C) (π/3┤+nπ;π/6+├ (k π)/2) n,k € ℤ
D) π/3+nπ, n € ℤ
E) π/3+kπ/2 , k € ℤ
8.Решите неравенство: 4 sin x cos x ≥ √2
A) π/8+πn ≤x ≤3π/8+πn , n € ℤ
B) π/8+πn - 1/2
A) π/12+πn/4
или проще
Пошаговое объяснение:
Вспомним формулу для разложения функции в ряд Тейлора
1 Запишем функцию
2 Найдем несколько производных:
...
3 Найдем общий вид производной:
У нас в любом случае будет производная произведения, тогда наша производная распадется на какое-то количество слагаемых либо просто синуса, либо просто косинуса и слагаемое с х умноженным на либо синус, либо косинус.
Заметим, что производная синуса равна
Тогда наше произведение в зависимости от n будет иметь разный вид.
Заметим, что всего различных слагаемых без множителя х будет n штук и все они будут иметь одинаковый знак
При n одинаковой четности знак один и тот же, в данной точке функция имеет вид
(производная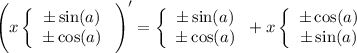 меняет местами функции)
меняет местами функции)
Мы можем записать для четных n знак у функции в виде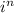 где i - мнимая единица, для нечетных n знак тоже можно записать в виде ее степени
где i - мнимая единица, для нечетных n знак тоже можно записать в виде ее степени 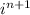
Для функции без множителя х формула такая (учитывая значения)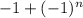 - мы должны будем еще умножить на степень для нечетных и также умножить на n (n раз брали производную)
- мы должны будем еще умножить на степень для нечетных и также умножить на n (n раз брали производную)
Для функции со множителем формула другая
Чтобы избавится от ненужных двоек в первом случае, умножим все на , и для того, чтобы все осталось как прежде во 2 случае, умножим только его часть на 2
, и для того, чтобы все осталось как прежде во 2 случае, умножим только его часть на 2
Тогда общая формула производной имеет вид
Можем вынести множитель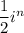 за скобки
за скобки
4 Тогда запишем ряд Тейлора
Начинаю с 1 так как писалась формула производной от 1.
f(2) = 2 * cos ( 2-2 ) = 2 * 1 = 2
Это и есть ответ
а)ε= √21/5 ; A(–5;0)
a=5
ε=c/a
c=ε·a=√21
b2=a2–c2=25–21=4
О т в е т.
(x2/25)+(y2/4)=1
б)A (√80;3) ,B(4 √6 ;3 √2)
Каноническое уравнение гиперболы
(x2/a2)–(y2/b2)=1
чтобы найти а и b подставляем координаты точек А и В:
{(80/a2)–(9/b2)=1
{(96/a2)–(18/b2)=1
Умножаем первое уравнение на (–2):
{–(160/a2)+(18/b2)=–2
{(96/a2)–(18/b2)=1
Складываем
–64/a2=–1
a2=64
18/b2=(96/a2)–1
b2=36
О т в е т. (x2/64)–(y2/36)=1
в)D: y=1
если каноническое уравнение параболы имеет вид
x2=–2py, то фокус параболы
F(0;–p/2)
D: y=p/2
Значит,
p/2=1
p=2
О т в е т. x2=–4y
Пошаговое объяснение: