№1. Берілген сөздердегі дауыссыз дыбыстар санының дауысты дыбыстар санына қатынасын тап. Қатынасты қысқартылған бөлшек түрінде жаз. Қарағанды 4 дауысты 5дауыссыз Жаратылыстану 7 дауыссыз 6 дауысты Құрылысшы 5 дауыссыз 4 дауысты Талапкер 5 дауыссыз 3 дауысты

ответ: (7/9); 0.875; (15/16); (16/17).

Объяснение:

есть такой прием - сравнение двух дробей с 1 или с (1/2)...

в общем случае, чтобы сравнить две обыкновенные дроби, нужно привести их к общему знаменателю...

если знаменатели одинаковые, то дробь тем больше, чем больше числитель...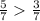

если числители одинаковые, то дробь тем больше, чем меньше знаменатель (обратная зависимость)...

...очень не хочется искать НОК(16;17) -это общий знаменатель...

на числовой прямой от числа (15/16) до 1 расстояние = (1/16);

от числа (16/17) до 1 расстояние = (1/17)... ,

т.е. 15/16 ближе к 0, а значит меньше...

7 / 9 = (7*16) / (9*16) = 112 / 144

15 / 16 = (15*9) / (16*9) = 135 / 144 > 7/9

0.875 = 875 / 1000 = 35 / 40 = 7 / 8 > 7 / 9

0.875 = 7 / 8 = 14 / 16 < 15 / 16

Отношением эквивалентности является

Отношением порядка не является

Пошаговое объяснение:

У этого отношения Т есть классы отношений

{1} - первый класс

{2,7,11} - второй класс. Здесь два делителя. Это простые числа, отличные от единицы

{4} - Третий класс. Здесь три делителя 1,2,4

{6, 8, 10} - Четвертый класс. Здесь четыре делителя. 1, и само число, отличное от единицы (6,8 или 10). Еще два делителя дополнительно.

У 6 - это 2 и 3.

У 8 - это 2 и 4.

У 10 - это 2 и 5.

Пошаговое объяснение:

Покажем, что это отношение эквивалентности.

Так как получили четыре класса эквивалентности.

Закон рефлексивности.

У каждого из классов эквивалентности выполняется рефлексивность

Среди первого класса 1~1

Среди второго класса

2~2

7~7

11~11

Среди третьего класса

4~4

Среди четвертого класса

6~6

8~8

10~10

Симметричность

Среди второго класса

2~7 и 7~2

2~11 и 11~2

Среди четвертого класса

6~8 и 8~6

10~8 и 8~10

10~6 и 6~10

Транзитивность

Среди второго класса

2~7

7~11, то из этого следует

2~11  или      11~2.

Выполняется.

Среди четвертого класса

6~8 и 8~10, то из этого следует 6~10.

В других классах транзитивность не нужна, так как там не более двух элементов.

У отношения порядка должна быть антисимметричность.

Проверим антисимметричность

Возьмем второй класс функций.

2~7 и 7~2 не влечет 2=7. Это не верно. Антисимметричность относительно Т не выполняется.

В отношении порядка должно быть: рефлексивность+антисимметричность+транзитивность

Здесь второй закон не выполняется.

Значит отношение порядка не выполняется.