1)агрохолдинг за год сократил площадь под посев капусты на 10%. а урожайность капусты за это время повысилась на 11%. больше или меньше стали собирать капусты в агрохолдинге по сравнению с годом? на сколько%. запишите решение и ответ. в пропорции 2)1 11/12+6*(2 5/12- 5/8): 18 3/7= в столбик по действиям
Заметим, что если у нас в какой-то момент времени на прямой оказалось точек, то после "удвоения" точек станет ровно
точек, то после "удвоения" точек станет ровно 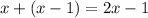 .
.
То есть, чтобы узнать, сколько точек было до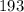 точек, нужно решить уравнение
точек, нужно решить уравнение 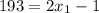 . Понятно, что
. Понятно, что 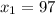 .
.
Узнаем, сколько точек было до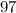 :
: 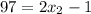 . Здесь
. Здесь 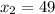 .
.
Очередным уравнением будет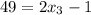 и
и 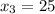 .
.
Далее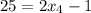 , откуда
, откуда 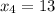 .
.
По аналогии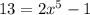 , и, конечно
, и, конечно 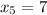 .
.
И, заключительный шаг,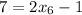 , где
, где 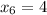 .
.
А уравнение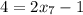 имеет ненатуральный корень
имеет ненатуральный корень  , точек на количество прямой не может быть дробным числом.
, точек на количество прямой не может быть дробным числом.
Получаем, что максимальное значение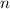 равно
равно 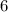 :
:
То есть, больше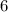 шагов нельзя сделать, иначе бы число точек на прямой было бы дробным.
шагов нельзя сделать, иначе бы число точек на прямой было бы дробным.
ответ:Будем разбивать на несколько случаев.
1) Если из первой урны взяли 4 чёрных шара. Вероятность достать четыре чёрных шара равна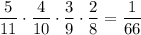 . Тогда во второй урне будет 3 белых и 9 черных шаров. Вероятность того, что среди трех отобранных шаров из второй урны окажутся все белые равна
. Тогда во второй урне будет 3 белых и 9 черных шаров. Вероятность того, что среди трех отобранных шаров из второй урны окажутся все белые равна 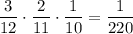 . По теореме умножения
. По теореме умножения 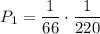
2) Если из первой урны взяли 1 белый шар и 3 чёрных. Вероятность такого события равна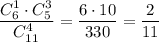 . Тогда во второй урне будет 4 белых и 8 черных шаров. Вероятность того, что среди отобранных шаров из второй урны все белые равна
. Тогда во второй урне будет 4 белых и 8 черных шаров. Вероятность того, что среди отобранных шаров из второй урны все белые равна 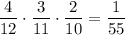 . По теореме умножения:
. По теореме умножения: 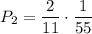
3) Из первой урны взяли 2 белых шара и 2 чёрных. Вероятность такого события: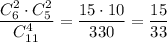 . Во второй урне будет 5 белых и 7 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны все окажутся белыми равна
. Во второй урне будет 5 белых и 7 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны все окажутся белыми равна 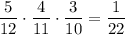 . По теореме умножения :
. По теореме умножения : 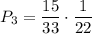
4) Из первой урны взяли 3 белых шара и 1 чёрный шар. Вероятность достать 3 белых шара и 1 чёрный шар равна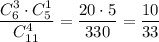 . Во второй урне останется 6 белых и 6 чёрных шаров. Вероятность того, что среди отобранных шаров из второй урны окажутся все белыми равна
. Во второй урне останется 6 белых и 6 чёрных шаров. Вероятность того, что среди отобранных шаров из второй урны окажутся все белыми равна 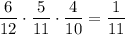 . По теореме умножения:
. По теореме умножения: 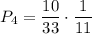
5) И, наконец, когда из первой урны урны взяли все четыре белых шаров. Вероятность такого события: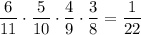 . Во второй урне остается 7 белых и 5 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны окажутся все белыми равна
. Во второй урне остается 7 белых и 5 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны окажутся все белыми равна 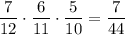 . По теореме умножения:
. По теореме умножения: 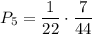
Итого, по теореме сложения: