Вберляндии плачевная ситуация с междугородним автобусным сообщением. во всей стране есть всего три автобусных маршрута, по каждому из которых курсирует лишь один автобус. в первый день нового года ровно в полночь все три автобуса отправляются по своим маршрутам из столицы берляндии. известно, что
первому автобусу на то, чтобы проехать весь маршрут и вернуться в столицу требуется a минут, второму — b минут, а третьему — c минут. таким образом, первый автобус отправляется из столицы берляндии в моменты времени 0, a, 2a, 3a, . ., второй — в моменты времени 0, b, 2b, 3b, . ., а третий в
моменты времени 0, c, 2c, 3c, . .. момент времени называется подходящим для пересадки, если в этот момент все три автобуса отправляются из столицы берляндии. например если a = 1, b = 2, c = 1, то моменты времени 0 и 2 являются подходящими для пересадки, а момент времени 1 не является, потому что в
этот момент времени второй автобус находится в пути. берляндия — особая страна с особым измерением времени, поэтому в берляндских сутках ровно t минут. это означает, что в первый день происходят все моменты времени с 0-го по (t−1)-й включительно, во второй день — c t-го по (2t−1)-й включительно, в
третий — с 2t-го по (3t − 1)-й включительно и так далее. министерство транспорта берляндии заинтересовалось, сколько подходящих для пересадки мо- ментов времени произойдёт в d-й день в берляндии. к сожалению, местные чиновники заняты другими делами, поэтому ответить на этот вопрос было поручено вам.
формат входных данных в пяти строках заданы пять целых чисел a, b, c, t и d (1 ⩽ a, b, c ⩽ 106 , 1 ⩽ t, d ⩽ 109 ) — время полного прохождения маршрута первым, вторым и третьим автобусами, соответственно, количество минут в сутках и номер дня, которым интересуется министерство транспорта берляндии.
формат выходных данных выведите одно целое число — количество подходящих для пересадки моментов времени в d-й день. примеры стандартный ввод стандартный вывод 1 2 1 3 1 2 2 3 4 7 2 1 2 3 4 3 3 0
Дано:
Найти: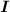 (информац.объём сообщения, кол-во информации в нём)
(информац.объём сообщения, кол-во информации в нём)
Находим количество информации в одном символе.
По сути, это минимальное количество двоичных разрядов, в котором можно хранить один символ нашего алфавита.
Выбирается оно из таблицы степеней двойки (первое значение, не меньшее, чем наше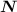 ), либо через формулу
), либо через формулу 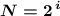 (подбирая минимальное подходящее
(подбирая минимальное подходящее 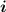 , либо решая уравнение через нахождение двоичного логарифма и затем округляя всегда с избытком, вверх).
, либо решая уравнение через нахождение двоичного логарифма и затем округляя всегда с избытком, вверх).
Пример подбора:
если , то
, то 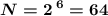 (алфавит из 64 символов можно хранить; для нас мало, надо минимум 107)
(алфавит из 64 символов можно хранить; для нас мало, надо минимум 107)
если , то
, то 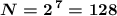 (алфавит из 128 символов можно хранить; для нас достаточно, это даже больше, чем наши 107 символов в алфавите)
(алфавит из 128 символов можно хранить; для нас достаточно, это даже больше, чем наши 107 символов в алфавите)
Выбираем минимальную подходящую степень= 7 (т.е. бит)
бит)
Пример расчёта:
отсюда, получаем что:
Можно считать одним из трёх : считать сам двоичный логарифм (если логарифм по произвольному основанию есть в вашем калькуляторе- во встроенном в Windows 10, в инженерном виде он есть например), или можно считать отношение десятичных либо натуральных логарифмов (см. дроби в расчёте). Десятичные либо натуральные логарифмы обычно есть в научных калькуляторах.
Получилось дробное значение, значит округляем до целого, но не как обычно, а всегда вверх (то есть, всегда берём целое число, большее чем наш результат). Так округляем потому, что нам нужно получить возможность хранить чуть больше символов, чем есть в нашем алфавите (раз уж ровно 107 не выходит).
Получаем, что: бит
бит
Далее, находим информационный объём сообщения:
ответ: 105 бит
Первая строка описывает импорт функции permutations из модуля itertools. Теперь мы можем ее использовать.
Далее, конструкция ''.join(b) используется для преобразования кортежа/массива в строку. Например, у нас есть кортеж ('1','2','3') и мы хотим получить из него строчку '123'. Для этого нам надо пройтись по каждому элементу кортежа и присоединять(по-английски join) их к изначально пустой строке. Проход по каждому элементу кортежа в данном случае описан как "({присоединение} for b in {собственно сам кортеж})", где b - элемент кортежа. Теперь про то, что здесь используют в качестве кортежа: permutations - с англ. значит перестановки. То есть, условно, у нас есть слово КОТ, применяем permutations(КОТ) и получаем такие вариации как КОТ, КТО, ОКТ, ОТК, ТКО, ТОК (само слово тоже учитывается, как и в задании).
Однако функция permutations возвращает все эти варианты перестановок как кортежи, то есть, как ('К', 'О', 'Т'), ('К', 'Т', 'О') и т.д. Поэтому-то мы и используем join, чтоб получить из кортежей строки для удобной работы. Теперь стоит заметить, что при наличии в слове одинаковых букв в вариациях перестановок могут получиться совпадающие позиции, так как для компьютера перестановка, например, в слове "ЛОТО" второй и четвертой буквы "О" будет давать новую вариацию, а для нас это все еще будет то же слово ЛОТО, ведь были поменяны местами две одинаковые буквы. Для избежания этой проблемы стоит прописать перед всем массивом с перестановками функцию set, которая просто уберет из него повторяющиеся элементы.
В следующей строке мы создаем массив только из тех строк полученного нами ранее массива с перестановками, которые удовлетворяют условию задания, а именно: не имеют одинаковых соседних букв. Почему это прописано как "if "ОО" not in b"(если "ОО" не в b)? Все просто: в перестановке слова ОДЕКОЛОН две соседние буквы могут быть только ОО, ведь у других букв банально нет пары. В итоге мы проходимся по каждому элементу нашего кортежа с вариациями, и смотрим есть ли в очередной вариации подстроки с двумя буквами О подряд. Если нет - то добавляем в массив, если есть - пропускаем.
В третьей строке выводится количество элементов (len(сокращение length - англ. длина) для массива - кол-во элементов в нем) в полученном массиве, то есть количество вариантов перестановок, где нет слов с одинаковыми соседними буквами.