С клавиатуры вводится 2 целых числа (a и b) и одно натуральное (n). Вывести на экран коэффициенты C_1, C_2 ... C_(n+1) разложения (ax+bx)^n=C_1x^n+C_2x^(n-1)y+...+C_(n+1)y^n.
Таким образом, , и для всех остальных коэффициентов
В ответ нужно вывести все коэффициенты для j = n.
Алгоритм: создадим список из n + 1 элемента, проинициализируем его так: a, b, 0, 0, ..., 0 (всего n - 1 ноль). Это коэффициенты разложения для j = 1. Затем в цикле будем обновлять значения, начиная с больших i.
Код (python 3):
a, b, n = map(int, input().split())
c = [a, b] + [0] * (n - 1)
for j in range(2, n + 1):
c[j] = b * c[j - 1]
for i in range(j - 1, 0, -1):
c[i] = a * c[i] + b * c[i - 1]
c[0] = a * c[0]
print(*c)
Пример ввода:
1 1 4
Пример вывода:
1 4 6 4 1
___________________________________________-
Можно сразу написать выражение для . Тогда, если вы умеете считать биномиальные коэффициенты, всё получается короче (и быстрее):
Пусть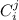 — коэффициент в разложении
— коэффициент в разложении 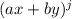 при
при 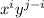 , то есть
, то есть
Выразим коэффициенты для j + 1 через j:
Таким образом, ,
, 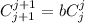 и для всех остальных коэффициентов
и для всех остальных коэффициентов 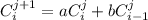
В ответ нужно вывести все коэффициенты для j = n.
Алгоритм: создадим список из n + 1 элемента, проинициализируем его так: a, b, 0, 0, ..., 0 (всего n - 1 ноль). Это коэффициенты разложения для j = 1. Затем в цикле будем обновлять значения, начиная с больших i.
Код (python 3):
a, b, n = map(int, input().split())
c = [a, b] + [0] * (n - 1)
for j in range(2, n + 1):
c[j] = b * c[j - 1]
for i in range(j - 1, 0, -1):
c[i] = a * c[i] + b * c[i - 1]
c[0] = a * c[0]
print(*c)
Пример ввода:
1 1 4
Пример вывода:
1 4 6 4 1
___________________________________________-
Можно сразу написать выражение для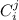 . Тогда, если вы умеете считать биномиальные коэффициенты, всё получается короче (и быстрее):
. Тогда, если вы умеете считать биномиальные коэффициенты, всё получается короче (и быстрее):
from math import comb
a, b, n = map(int, input().split())
for i in range(n + 1):
print(comb(n, i) * a**i * b**(n - i), end=" ")