Перевод из pascal в qbasic program dekio; varnstr : string; i,ksl : integer; beginksl: =0; writeln('введите строку'); readln(nstr); for i: =1 to length(nstr) doif (nstr[i]='.') or (nstr[i]=' ') theninc(ksl); writeln('количество слов ',ksl); end.
Для того, чтобы решить задачу, нам не требуется делать какие-то сложные переборы в поисках кратчайшего пути. Так как на поле у нас нет никаких препятствий, нам достаточно рассчитать расстояние между клетками поля. Это и будет ответом.
Как рассчитать расстояние
Для этого используются метрики.
Мне тут давеча сказали, что это слово пугает детей и вводит их в паническое состояние.
¯\_(ツ)_/¯ Не понимаю, чего там такого пугающего)
На самом деле, тут всё просто, так что забудем про страшные слова и посмотрим, как можно вычислять расстояния.
Для примера возьмём плоскость, на которой нам достаточно 2-х координат для задания положения точек.
Как посчитать расстояние между точкой А(x0, y0) и B(x1, y1)?
Уроки геометрии учат, что . Поздравляю, ты познакомился со своей первой метрикой. Она называется Евклидова метрика. Или Евклидово расстояние - кратчайшее расстояние между двумя точками пространства.
А теперь представим, что ты оказался в центре города. И тебе надо узнать, как много нужно пройти от твоего местоположения до гостиницы. Путь это будут всё те же точки A и B.
Мы уже могли бы рассчитать Евклидову метрику. Однако она нам мало чем мы ведь не можем ходить насквозь домов. Придётся обходить. А значит, и расстояние увеличится.
Для такой ситуации подходит Манхэттенская метрика или по-другому Расстояние городских кварталов.
Рассчитывается она тоже просто . То есть просто сумма расстояний по x и по y. Если ходить по улицам, не через дворы, то нам не важно, сколько раз мы будем поворачивать. Мы пройдем столько же, сколько бы сначала по x, а потом по y.
Помимо этих двух метрик, есть ещё метрика Чебышёва.
Она рассчитывается как . То есть вычисляются расстояния по координатам, и выбирается максимальное из них.
Забавно, но одно из объяснений этой метрики звучит как "Минимальное количество ходов, которое требуется совершить королю из клетки A в клетку B".
Ниже я привел картинку, на которой можно увидеть, почему это работает.
Итак, решено. Будем рассчитывать искомое расстояние по методу Чебышёва.
КодProgram king;Varx0, y0, x1, y1: integer;BeginWriteln('Введите координаты точки s:');Readln(x0, y0);Writeln('Введите координаты точки f:');Readln(x1, y1);If ((a < 1) or (a > 8) or (b < 1) or (b > 8) or (c < 1) or (c > 8) or (d < 1) or (d > 8)) thenWriteln('Ошибка! Проверьте правильность введённых данных! Закрытие программы... ')ElseWriteLn(Max(Abs(x1 - x0), Abs(y1 - y0)));Readln;End.
Для того, чтобы решить задачу, нам не требуется делать какие-то сложные переборы в поисках кратчайшего пути. Так как на поле у нас нет никаких препятствий, нам достаточно рассчитать расстояние между клетками поля. Это и будет ответом.
Как рассчитать расстояниеДля этого используются метрики.
Мне тут давеча сказали, что это слово пугает детей и вводит их в паническое состояние.
¯\_(ツ)_/¯ Не понимаю, чего там такого пугающего)
На самом деле, тут всё просто, так что забудем про страшные слова и посмотрим, как можно вычислять расстояния.
Для примера возьмём плоскость, на которой нам достаточно 2-х координат для задания положения точек.
Как посчитать расстояние между точкой А(x0, y0) и B(x1, y1)?
Уроки геометрии учат, что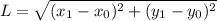 . Поздравляю, ты познакомился со своей первой метрикой. Она называется Евклидова метрика. Или Евклидово расстояние - кратчайшее расстояние между двумя точками пространства.
. Поздравляю, ты познакомился со своей первой метрикой. Она называется Евклидова метрика. Или Евклидово расстояние - кратчайшее расстояние между двумя точками пространства.
А теперь представим, что ты оказался в центре города. И тебе надо узнать, как много нужно пройти от твоего местоположения до гостиницы. Путь это будут всё те же точки A и B.
Мы уже могли бы рассчитать Евклидову метрику. Однако она нам мало чем мы ведь не можем ходить насквозь домов. Придётся обходить. А значит, и расстояние увеличится.
Для такой ситуации подходит Манхэттенская метрика или по-другому Расстояние городских кварталов.
Рассчитывается она тоже просто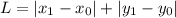 . То есть просто сумма расстояний по x и по y. Если ходить по улицам, не через дворы, то нам не важно, сколько раз мы будем поворачивать. Мы пройдем столько же, сколько бы сначала по x, а потом по y.
. То есть просто сумма расстояний по x и по y. Если ходить по улицам, не через дворы, то нам не важно, сколько раз мы будем поворачивать. Мы пройдем столько же, сколько бы сначала по x, а потом по y.
Помимо этих двух метрик, есть ещё метрика Чебышёва.
Она рассчитывается как . То есть вычисляются расстояния по координатам, и выбирается максимальное из них.
. То есть вычисляются расстояния по координатам, и выбирается максимальное из них.
Забавно, но одно из объяснений этой метрики звучит как "Минимальное количество ходов, которое требуется совершить королю из клетки A в клетку B".
Ниже я привел картинку, на которой можно увидеть, почему это работает.
Итак, решено. Будем рассчитывать искомое расстояние по методу Чебышёва.
КодProgram king;Varx0, y0, x1, y1: integer;BeginWriteln('Введите координаты точки s:');Readln(x0, y0);Writeln('Введите координаты точки f:');Readln(x1, y1);If ((a < 1) or (a > 8) or (b < 1) or (b > 8) or (c < 1) or (c > 8) or (d < 1) or (d > 8)) thenWriteln('Ошибка! Проверьте правильность введённых данных! Закрытие программы... ')ElseWriteLn(Max(Abs(x1 - x0), Abs(y1 - y0)));Readln;End.program shkisvf;
uses
crt;
procedure minh(sx, sy, dx, dy: integer);
var
h: integer;
begin
h := 0;
while ((sx <> dx) and (sy <> dy)) do
begin
if (sx < dx) and (sy < dy) then
begin
sx := sx + 1;
sy := sy + 1;
h := h + 1;
end ;
if (sx > dx) and (sy < dy) then
begin
sx := sx - 1;
sy := sy + 1;
h := h + 1;
end ;
if (sx < dx) and (sy > dy) then
begin
sx := sx + 1;
sy := sy - 1;
h := h + 1;
end ;
if (sx > dx) and (sy > dy) then
begin
sx := sx - 1;
sy := sy - 1;
h := h + 1;
end ;
end;
while ((sx <> dx) or (sy <> dy)) do
begin
if sx < dx then
begin
sx := sx + 1;
h := h + 1;
end ;
if sx > dx then
begin
sx := sx - 1;
h := h + 1;
end ;
if sy < dy then
begin
sy := sy + 1;
h := h + 1;
end ;
if sy > dy then
begin
sy := sy - 1;
h := h + 1;
end ;
end;
writeln('Минимальное количество ходов: ', h);
end;
procedure cheb(sx, sy, dx, dy: integer);
var
max, rx, ry: integer;
begin
rx := abs(sx - dx);
ry := abs(sy - dy);
writeln('Минимальное кол-во ходов по Чебышёву:');
if rx > ry then
writeln(rx)
else
writeln(ry);
end;
var
a, b, c, d: integer;
begin
writeln('Введите координаты точки s:');
readln(a, b);
writeln('Введите координаты точки f:');
readln(c, d);
if ((a < 1) or (a > 8) or (b < 1) or (b > 8) or (c < 1) or (c > 8) or (d < 1) or (d > 8)) then
writeln('Ошибка! Проверьте правильность введённых данных! Закрытие программы... ')
else
minh(a, b, c, d);
cheb(a, b, c, d);
readln;
end.