Какой алгоритм, предназначенный для поиска минимального пути между двумя вершинами во взвешенном графе с наличием отрицательных ребер, обладает наилучшей производительностью, если ребер много меньше, чем вершин (требования по памяти не учитываются)? a. алгоритм поиска в ширину
b. алгоритм Беллмана-Форда
c. алгоритм Дейкстры
d. алгоритм Флойда
e. все варианты обладают равной оценкой по производительности

Дано:               |    Решение:

i = 16 бит          |       ΔI = 20 байт = 160 бит

ΔI = 20 байт   |      Вспомним, что I = k*i, тогда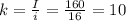  

Слово - ?               Значит, из текста удалили 10 символов

                              В слове "Виннипег" 8 символов, но не будем забывать,  

                               что помимо слова нам ещё нужно убрать одну запятую

                              и один пробел. Итог - 10 символов

                                                                                                 ответ: Виннипег

#include <iostream>

#include <string>

bool is_palindrome(const std::string& s) {

   std::string r(s);

   std::reverse(r.begin(), r.end());

   return s == r;

}

int main() {

   std::string s1,s2;

   setlocale(LC_ALL, "Russian");

   std::cout << "Введите число 1: ";

   std::getline(std::cin, s1);

   std::cout << "Введите число 2: ";

   std::getline(std::cin, s2);

   if (is_palindrome(s1)|| is_palindrome(s2))

       std::cout << "Одно из введенных чисел является палиндромом " << std::endl;

   else

       std::cout << "Ни одно из введенных чисел не является палиндромом " << std::endl;

   return 0;

}