Составим математическую модель. Заметим, что каждый раз текущая сумма умножается на некоторое число , где r — процент. То есть начальная сумма вклада S и конечная сумма вклада F связаны следующим отношением: , где x — срок вклада. Его можно выразить следующим образом:
Если результат получается не целым, нужно округлять вверх, иначе сумма будет недоставать от необходимой.
Защиту от дурака, например, проверка на 0, отрицательные значения, делать не будем, считаем, что все данные введены корректно.
Алгоритм:
Составим математическую модель. Заметим, что каждый раз текущая сумма умножается на некоторое число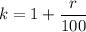
, где r — процент. То есть начальная сумма вклада S и конечная сумма вклада F связаны следующим отношением: 
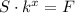, где x — срок вклада. Его можно выразить следующим образом:
Если результат получается не целым, нужно округлять вверх, иначе сумма будет недоставать от необходимой.
Защиту от дурака, например, проверка на 0, отрицательные значения, делать не будем, считаем, что все данные введены корректно.
Программа:
from math import log, ceil
start_s = float(input())
finish_s = float(input())
k = 1.05 #percent
print(ceil(log(finish_s / start_s, k)))
Объяснение:
Python
# подключаем модуль, чтобы в ручную не вводить матрицу
from random import randint
# вводим размерность матрицы
n,m=map(int, input('Введите размерность матрицы n m:').split())
# заполняем матрицу случайными числами в диапазоне (-20,20)
a=[[randint(10,99) for j in range(n)] for i in range(m)]
# печатаем матрицу построчно, чтобы было понятно и красиво
for i in a: print(i)
# зададим стартовое минимальное и максимальное значение
# присвоим им первый элемент матрицы
minA = a[0][0]
maxA = a[0][0]
# найдём в каждом столбце минимум и максимум
for i in range(m):
# минимум текущего столбца будет < нашего minA
if min(a[i]) < minA:
# то переприсвоим минимум
minA=min(a[i])
# аналогично с максимумом
if max(a[i]) > maxA:
maxA=max(a[i])
# выводим на печать минимум и максимум
print('min=', minA)
print('max=', maxA)