Хочу с у знающих людей. Ноут греется во время работы, если я оставлю дно(оно сьемное) над процессором открытым это повлияет на его спад температуры или ничего не произойдёт? Заранее
Подписываюсь под каждым словом объяснения @Nelle987.
Заданные значения x = a+b и y = ab - подходят под описание теоремы Виета. А значит, мы можем свести задачу к поиску корней квадратного уравнения в целых действительных числах.
Хочу дополнить ответ @Nelle987 другой реализацией целочисленного квадратного корня, работающего на этапе компиляции.
Код:
#include <iostream>constexpr long long isqrt (long long value, long long sq = 1ll, long long dlt = 3ll){ return sq <= value ? isqrt(value, sq+dlt, dlt+2ll) : (dlt >> 1) - 1ll;}int main() { long long x, y; std::cin >> x >> y; auto d = x * x - 4 * y; if (d < 0) { std::cout << 0; return 0; } auto sqrt_d = isqrt(d); if (sqrt_d * sqrt_d != d) { std::cout << 0; return 0; } if ((x - sqrt_d) % 2 != 0) { std::cout << 0; return 0; } std::cout << (x - sqrt_d) / 2 << " " << (x + sqrt_d) / 2; return 0;}
Вам нужно найти такие a и b, что a + b = x и ab = y. По теореме Виета a и b - корни уравнения . Находим дискриминант , если он отрицательный - у уравнения не то что натуральных, действительных решений нет. Если дискриминант неотрицательный, но не полный квадрат, то натуральных решений тоже нет. Иначе решения уравнения , если они натуральные - это и есть ответ.
У меня нет уверенности, что можно посчитать целый корень из большого натурального числа с стандартных функций, так что напишу свою реализацию на основе двоичного поиска.
[Del me plz]
Подписываюсь под каждым словом объяснения @Nelle987.
Заданные значения x = a+b и y = ab - подходят под описание теоремы Виета. А значит, мы можем свести задачу к поиску корней квадратного уравнения в целых действительных числах.
Хочу дополнить ответ @Nelle987 другой реализацией целочисленного квадратного корня, работающего на этапе компиляции.
Код:
#include <iostream>constexpr long long isqrt (long long value, long long sq = 1ll, long long dlt = 3ll){ return sq <= value ? isqrt(value, sq+dlt, dlt+2ll) : (dlt >> 1) - 1ll;}int main() { long long x, y; std::cin >> x >> y; auto d = x * x - 4 * y; if (d < 0) { std::cout << 0; return 0; } auto sqrt_d = isqrt(d); if (sqrt_d * sqrt_d != d) { std::cout << 0; return 0; } if ((x - sqrt_d) % 2 != 0) { std::cout << 0; return 0; } std::cout << (x - sqrt_d) / 2 << " " << (x + sqrt_d) / 2; return 0;}Вам нужно найти такие a и b, что a + b = x и ab = y. По теореме Виета a и b - корни уравнения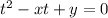
. Находим дискриминант 
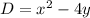, если он отрицательный - у уравнения не то что натуральных, действительных решений нет. Если дискриминант неотрицательный, но не полный квадрат, то натуральных решений тоже нет. Иначе решения уравнения 
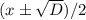, если они натуральные - это и есть ответ.
У меня нет уверенности, что можно посчитать целый корень из большого натурального числа с стандартных функций, так что напишу свою реализацию на основе двоичного поиска.
#include <iostream>
#include <cmath>
long long isqrt(long long number) {
long long answer = 0, left = 0, right = 1e9;
while (left <= right) {
long long middle = (left + right) / 2;
long long middle_squared = middle * middle;
if (middle_squared == number) {
return middle;
} else if (middle_squared < number) {
answer = middle;
left = middle + 1;
} else {
right = middle - 1;
}
}
return answer;
}
int main() {
long long x, y;
std::cin >> x >> y;
auto d = x * x - 4 * y;
if (d < 0) {
std::cout << 0;
return 0;
}
auto sqrt_d = isqrt(d);
if (sqrt_d * sqrt_d != d) {
std::cout << 0;
return 0;
}
if ((x - sqrt_d) % 2 != 0) {
std::cout << 0;
return 0;
}
std::cout << (x - sqrt_d) / 2 << " " << (x + sqrt_d) / 2;
}