Мы знаем координаты двух точек, лежащих на прямой. Обозначим их как и . Тогда:
Решение
Мы знаем координаты точек многоугольника.
Для каждого ребра (пары соседних точек) мы должны проверить, чтобы все остальные точки находились по одну сторону от прямой, которой принадлежит эта пара точек.
Т.е., мы перебираем каждое ребро и смотрим, чтобы остальные точки были одного знака.
Оказывается, смотреть все точки необязательно! Нам нужно проверить каждое ребро, чтобы сказать ответ. Поэтому, нам достаточно смотреть лишь положение двух соседних с этим ребром точек относительно ребра.
Итого, мы должны для каждого ребра убедиться, что две соседних с этим ребром точки лежат по одну сторону от ребра. Вот и всё.
Код
#include <bits/stdc++.h>
using namespace std;
int main() {
int n;
cin >> n;
long double x[n+2];
long double y[n+2];
for (int i = 0; i < n; i++) {
cin >> x[i] >> y[i];
}
x[n] = x[0];
y[n] = y[0];
x[n+1] = x[1];
y[n+1] = y[1];
for (int i = 1; i < n; i++) {
long double a = y[i+1] - y[i];
long double b = x[i] - x[i+1];
long double c = y[i] * x[i+1] - x[i]*y[i+1];
if ((a*x[i-1]+b*y[i-1]+c)*(a*x[i+2]+b*y[i+2]+c) < 0) {
#include <iostream>
#include <iterator>
#include <vector>
using namespace std;
int main() {
int n = 5;
int m = 6;
vector<vector<int>> a(n, vector<int>(m));
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j)
cin >> a[i][j];
}
vector<double> ans(m);
for (int i = 0, q = 0; i < m; ++i, ++q) {
int sum = 0;
int cnt = 0;
for (int j = 0; j < n; ++j) {
if (a[j][i] < 0) {
sum += a[j][i];
++cnt;
}
}
if (sum)
ans[q] = sum / (double)cnt;
}
copy(ans.cbegin(), ans.cend(), ostream_iterator<double>(cout, " "));
}
Общее уравнение прямой: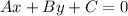
Мы знаем координаты двух точек, лежащих на прямой. Обозначим их как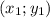 и
и 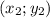 . Тогда:
. Тогда:
Решение
Мы знаем координаты точек многоугольника.
Для каждого ребра (пары соседних точек) мы должны проверить, чтобы все остальные точки находились по одну сторону от прямой, которой принадлежит эта пара точек.
Т.е., мы перебираем каждое ребро и смотрим, чтобы остальные точки были одного знака.
Оказывается, смотреть все точки необязательно! Нам нужно проверить каждое ребро, чтобы сказать ответ. Поэтому, нам достаточно смотреть лишь положение двух соседних с этим ребром точек относительно ребра.
Итого, мы должны для каждого ребра убедиться, что две соседних с этим ребром точки лежат по одну сторону от ребра. Вот и всё.
Код
#include <bits/stdc++.h>
using namespace std;
int main() {
int n;
cin >> n;
long double x[n+2];
long double y[n+2];
for (int i = 0; i < n; i++) {
cin >> x[i] >> y[i];
}
x[n] = x[0];
y[n] = y[0];
x[n+1] = x[1];
y[n+1] = y[1];
for (int i = 1; i < n; i++) {
long double a = y[i+1] - y[i];
long double b = x[i] - x[i+1];
long double c = y[i] * x[i+1] - x[i]*y[i+1];
if ((a*x[i-1]+b*y[i-1]+c)*(a*x[i+2]+b*y[i+2]+c) < 0) {
cout << "NO" << endl;
return 0;
}
}
cout << "YES" << endl;
return 0;
}