Дан массив размера N. Найти номер его первого локального минимума (локальный минимум — это элемент, который меньше любого из своих
соседей). Решение на Питоне

1)

var

a,b:array [1..100] of integer;

i,j,k,a,b,f:integer;

begin

randomize;

readln(a);

readln(b);

k:=0;

for i:=1 to 20 do

begin

a[i]:=random(135)-45;

f:=0;

for j:=a to b do

if (a[i]=j) and (a[i] mod 7 =0) then f:=1;

if f=0 then

begin

k:=k+1;

b[k]:=a[i];

end;

end;

for i:=1 to k do

writeln(b[i]);

end.

2)

var

a,b:array [1..100] of integer;

i,j,k:integer;

begin

randomize;

readln(k);

j:=0;

for i:=1 to 20 do

begin

a[i]:=random(135)-45;

writeln(a[i]);

for i:=1 to 19 do

begin

if a[i]*a[i+1]>0 then

begin

j:=j+1;

b[j]:=a[i];

j:=j+1;

b[j]:=k;

end

else

begin

j:=j+1;

b[j]:=a[i];

end;

end;

j:=j+1;

b[j]:=a[20];

for i:=1 to j do

writeln(b[j]);

 

3)

var

a,b:array [1..20] of integer;

i,j,k1,k2:integer;

begin

randomize;

readln(k1);

readln(k2);

if k1<k2 then

begin

for i:=1 to 20 do

begin

a[i]:=random(135)-45;

writeln(a[i]);

end;

for i:=1 to k1-1 do

b[i]:=a[i];

for i:=k2+1 to 20 do

b[i]:=a[i];

j:=k2;

for i:=k1 to k2 do

begin

b[j]:=a[i];

j:=j-1;

end;

for i:=1 to 20 do

writeln(b[i]);

end;

end.

 

Применим метод уменьшения в два раза области неопределенности(путь к стелажу выделен жирным шрифтом):

16

8-8

4-4 4-4

2-2 2-2 2-2 2-2

1-1 1-1 1-1 1-1 1-1 1-1 1-1 1-1

МЫ потратили 4 бита информации на поиск нужного стеллажа, теперь нащдо найти нужную нам полку:

6

3-3

2-1 2-1 

1-1 1 1-1 1

Потрачено еще 3 бита информации. Всего информации 4+3 равно 7 бит информации Воспользуемся формулой: 2

2^i=N

 

Количество информации о нахождении стеллажа:

 

2^4=16

 

i=4 бита

 

Количество информации о нахождении полки:

 

2^i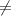6 поэтому возьмем число 2^i так чтобы результат находился рядом с числом 6. Так как если число будет меньше 6 то мы не сможем точно получить информация, то 2^i должно быть больше 6. Значит:

2^3=8

 

I=3

 

4+3=7 бит информации