Объяснение:
1) cosa = AB/AC
AC = BC/sina
sinC = cosa
2) 3(sin^2 + cos^2) = 3*1 = 3
3) sina = 3cosa |: cosa
tga = 3
5) Т.к. не указаны промежутки на которых определен угол а, то будет два случая
sina = -√(1 - cos^2) = -0,6, тогда tga = -0,6/0,8 = -0,75
sinа = √(1 - cos^2) = 0,6, тогда tga = 0,6/0,8 = 0,75
6) У р/б трапеции ABCD ВС - малое основание, AD - большое. Проведем две высоты из ВН и СН1 к AD. Они делят трапецию на прямоугольник и два равных прямоугольных тр-ка
АН1 = (8-2)/2 = 3
h = BH = 3*tga
Боковая сторона трапеции = 3/cosa
Дано: треугольник АВС, ∠ABC = 60°, AB=√3, BC=2√3, BE - биссектриса.
Найти:BE
Рассмотрим треугольник АВС.
По теореме косинусов:
AC²=AB²+BC²-2AB*BC*cos∠B
AC² = 3 + 12 - 2*2√3*√3*0,5
AC²=15-6
AC²=9
AC=3 см
Все из того же треугольника ABC по теореме косинусов:
AB²=BC²+AC²-2*BC*AC * cos∠C
3=12+9 - 2*3*2√3 cos∠C
3=21-12√3cos∠C
12√3cos∠C=18
cos∠C = 18/12√3 = 3/2√3
Значит, cos∠C= 3/2√3
Избавимся от иррациональности в знаменателе (домножим числитель и знаменатель дроби на √3)
cos∠C = 3√3/6
Cos∠C = √3/2
∠C = 30°
∠A = 180°-∠B-∠C=180°-60°-30°=90°
Видим, что ∠А - прямой, а это значит, что треугольник АВС - прямоугольный
∠ABE = 1/2 ∠ABC = 1/2*60°=30°
Рассмотрим ΔABE (∠A=90°)
cos∠B =
cos30° = √3 / BE
√3/2 = √3/BE
Значит, ВЕ = 2 см
ответ: ВЕ=2 см
Объяснение:
1) cosa = AB/AC
AC = BC/sina
sinC = cosa
2) 3(sin^2 + cos^2) = 3*1 = 3
3) sina = 3cosa |: cosa
tga = 3
5) Т.к. не указаны промежутки на которых определен угол а, то будет два случая
sina = -√(1 - cos^2) = -0,6, тогда tga = -0,6/0,8 = -0,75
sinа = √(1 - cos^2) = 0,6, тогда tga = 0,6/0,8 = 0,75
6) У р/б трапеции ABCD ВС - малое основание, AD - большое. Проведем две высоты из ВН и СН1 к AD. Они делят трапецию на прямоугольник и два равных прямоугольных тр-ка
АН1 = (8-2)/2 = 3
h = BH = 3*tga
Боковая сторона трапеции = 3/cosa
Дано: треугольник АВС, ∠ABC = 60°, AB=√3, BC=2√3, BE - биссектриса.
Найти:BE
Рассмотрим треугольник АВС.
По теореме косинусов:
AC²=AB²+BC²-2AB*BC*cos∠B
AC² = 3 + 12 - 2*2√3*√3*0,5
AC²=15-6
AC²=9
AC=3 см
Все из того же треугольника ABC по теореме косинусов:
AB²=BC²+AC²-2*BC*AC * cos∠C
3=12+9 - 2*3*2√3 cos∠C
3=21-12√3cos∠C
12√3cos∠C=18
cos∠C = 18/12√3 = 3/2√3
Значит, cos∠C= 3/2√3
Избавимся от иррациональности в знаменателе (домножим числитель и знаменатель дроби на √3)
cos∠C = 3√3/6
Cos∠C = √3/2
∠C = 30°
∠A = 180°-∠B-∠C=180°-60°-30°=90°
Видим, что ∠А - прямой, а это значит, что треугольник АВС - прямоугольный
∠ABE = 1/2 ∠ABC = 1/2*60°=30°
Рассмотрим ΔABE (∠A=90°)
cos∠B =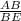
cos30° = √3 / BE
√3/2 = √3/BE
Значит, ВЕ = 2 см
ответ: ВЕ=2 см