1) Из рисунка следует, что внутренние стороны треугольников основания являются средними линиями большого треугольника, так как соединяют середины сторон, и, следовательно, равны:
1/2 стороны, обозначенной 2 штрихами (у серого треугольника);
1/2 стороны, обозначенной 1 штрихом (у белого треугольника).
Таким образом, 3 стороны белого треугольника равны 3 сторонам серого треугольника, - значит, эти треугольники равны.
2) Фигура, обозначенная S, является параллелограммом, так как его противоположные стороны равны (это вытекает из выше доказанного равенства треугольников) и параллельны (средние линии параллельны основаниям). Следовательно, S в 2 раза больше площади серого треугольника:
Поскольку пирамида правильная, то BH - медиана, биссектриса и высота треугольника ABC, то есть верно, что . Проведем прямую . Тогда . Пусть CP другая медиана треугольника ABC. Пусть медианы этого треугольника пересекаются в точке O. Тогда из-за того, что пирамида правильная, SO - это ее высота, т.е. , а значит и любой прямой в этой плоскости. Пусть . Проведем через точку J прямую параллельную SO, которая пересечет SC в точке I. Тогда , а значит и любой прямой в этой плоскости. Соединим точки M, I и E. Получим плоскость . Покажем, что . и , и . Тогда задача сводится к нахождению площади треугольника . Будем искать ее, как . Из подобия треугольников следует, что . Из подобия треугольников . Подставив найденное в формулу выше, получим . Таким нами образом было получено, что искомая площадь равна .
26
Объяснение:
1) Из рисунка следует, что внутренние стороны треугольников основания являются средними линиями большого треугольника, так как соединяют середины сторон, и, следовательно, равны:
1/2 стороны, обозначенной 2 штрихами (у серого треугольника);
1/2 стороны, обозначенной 1 штрихом (у белого треугольника).
Таким образом, 3 стороны белого треугольника равны 3 сторонам серого треугольника, - значит, эти треугольники равны.
2) Фигура, обозначенная S, является параллелограммом, так как его противоположные стороны равны (это вытекает из выше доказанного равенства треугольников) и параллельны (средние линии параллельны основаниям). Следовательно, S в 2 раза больше площади серого треугольника:
S = 13 · 2 = 26
(см. объяснение)
Объяснение:
Поскольку пирамида правильная, то BH - медиана, биссектриса и высота треугольника ABC, то есть верно, что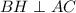 . Проведем прямую
. Проведем прямую 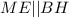 . Тогда
. Тогда 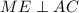 . Пусть CP другая медиана треугольника ABC. Пусть медианы этого треугольника пересекаются в точке O. Тогда из-за того, что пирамида правильная, SO - это ее высота, т.е.
. Пусть CP другая медиана треугольника ABC. Пусть медианы этого треугольника пересекаются в точке O. Тогда из-за того, что пирамида правильная, SO - это ее высота, т.е. 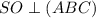 , а значит и любой прямой в этой плоскости. Пусть
, а значит и любой прямой в этой плоскости. Пусть  . Проведем через точку J прямую параллельную SO, которая пересечет SC в точке I. Тогда
. Проведем через точку J прямую параллельную SO, которая пересечет SC в точке I. Тогда 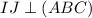 , а значит и любой прямой в этой плоскости. Соединим точки M, I и E. Получим плоскость
, а значит и любой прямой в этой плоскости. Соединим точки M, I и E. Получим плоскость 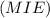 . Покажем, что
. Покажем, что 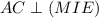 .
. 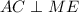 и
и 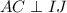 , и
, и 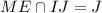 . Тогда задача сводится к нахождению площади треугольника
. Тогда задача сводится к нахождению площади треугольника 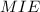 . Будем искать ее, как
. Будем искать ее, как 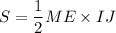 . Из подобия треугольников следует, что
. Из подобия треугольников следует, что 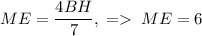 . Из подобия треугольников
. Из подобия треугольников 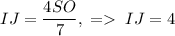 . Подставив найденное в формулу выше, получим
. Подставив найденное в формулу выше, получим 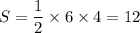 . Таким нами образом было получено, что искомая площадь равна
. Таким нами образом было получено, что искомая площадь равна 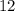 .
.
Задание выполнено!