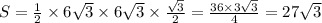Написать объяснение сложнее, чем показать... я нарисовала... нужно просто рассмотреть углы во всех получившихся треугольниках... и, между прочим, выяснится, что треугольники АОЛ (у меня АОМ))) и ВОК подобны... начало рассуждений: около 4-угольника МОЖНО описать окружность, если сумма его противоположных углов = 180 градусов... т.е. нужно доказать, что: А+90+у = 180 и В+90+х = 180 ------------------------------------------------- одновременно, т.е. это система... а решая систему, можно складывать оба уравнения... и получится, что нужно доказать равенство: А+В+х+у = 180 а это становится очевидно из "отрезанного" треугольника CКМ оказывается С=х+у а сумма углов данного треугольника А+В+С = 180 ч.и.т.д.
Углы ABO, CBO равны, т.к. BO - биссектриса, аналогично равны углы BCO и OCA; Дуги AP и PC равны => AP=PC => углы PAC и ACP равны. Угол ABP равен углу ACP, так как они опираются на одну дугу.
1) Выразим через x и y угол PCO: PCO=x+y; Теперь угол POC: POC=180-BOC; BOC=180-x-y => POC=180-(180-x-y)=x+y; Значит PCO=POC что и требовалось.
2) Из доказанного ранее, что не умаляет очевидности этого факта, AP=PC; Так как угол ABC = 120, то угол APC=60; Следовательно треугольник APC является равносторонним. Найдем AC по известной формуле: ; Площадь треугольника APC:
я нарисовала...
нужно просто рассмотреть углы во всех получившихся треугольниках...
и, между прочим, выяснится, что треугольники
АОЛ (у меня АОМ))) и ВОК подобны...
начало рассуждений:
около 4-угольника МОЖНО описать окружность,
если сумма его противоположных углов = 180 градусов...
т.е. нужно доказать, что:
А+90+у = 180 и В+90+х = 180
-------------------------------------------------
одновременно, т.е. это система...
а решая систему, можно складывать оба уравнения...
и получится, что нужно доказать равенство: А+В+х+у = 180
а это становится очевидно из "отрезанного" треугольника CКМ
оказывается С=х+у
а сумма углов данного треугольника А+В+С = 180
ч.и.т.д.
Все обозначения на рисунке.
Углы ABO, CBO равны, т.к. BO - биссектриса, аналогично равны углы BCO и OCA; Дуги AP и PC равны => AP=PC => углы PAC и ACP равны. Угол ABP равен углу ACP, так как они опираются на одну дугу.
1) Выразим через x и y угол PCO: PCO=x+y; Теперь угол POC: POC=180-BOC; BOC=180-x-y => POC=180-(180-x-y)=x+y; Значит PCO=POC что и требовалось.
2) Из доказанного ранее, что не умаляет очевидности этого факта, AP=PC; Так как угол ABC = 120, то угол APC=60; Следовательно треугольник APC является равносторонним. Найдем AC по известной формуле: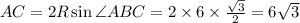 ; Площадь треугольника APC:
; Площадь треугольника APC: