Задания
Найдите расстояние между точками М и N, если М(-1;3), N(2;-4).
Найдите координату точки Х, которая является серединой отрезка MN. [2]
а) Напишите уравнение окружности с центром в точке К(11;-4) и радиусом 17. [1]
b) Выясните, как расположена точка Н(-6;-8) относительно окружности, заданной уравнением пункта а. [1]
Постройте окружность, заданную уравнением (х+4)2+(у-1)2=16. [2]
Точки А(-4;-3), В(-4;5), С(2;5), D(8;-3) – вершины прямоугольной трапеции с основаниями ВC и АD. Найдите длину средней линии и уравнение диагонали АС заранее большое
ну смотри, угол между прямой и плоскостью, это угол между её проекцией и этой прямой, у тебя же дан косинус угла, если его сократить получится 24/25, у тебя дан прилежащий катет, ты можешь найти гипотенузу:
24/25 = 48/x где - х это гипотенуза
x = 50
так как у тебя даже сказано "перпендикуляр" значит треугольник прямоугольный, ну по теореме пифагора найди, то есть гипотенуза в квадрате минус катет (который равен 48 по условию) в квадрате и всё это под корнем будет равно 14 ( ну это 50 в квадрате - 48 в квадрате и всё это под корнем)
вторая аналогично.
извиняюсь за текст, пишу с компа, телефон без зарядки)
Раз речь идёт об отрезках на осях координат, то уравнение плоскости надо рассматривать в форме, называемой "в отрезках".
Такое уравнение имеет вид: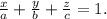
Здесь a, b c - отрезки на осях Ох, Оу и Оz, отсекаемые плоскостью.
Примем равные а и в за "к".
Получим уравнение плоскости (x/k) + (y/k) + (z/c) = 1.
Приведём к общему знаменателю.
cx + cy + kz = kc и подставим координаты заданных точек.
c3 + c5 + k1 = kc 8c +k = kc, (1)
c7 + c7 + k8 = kc 14c + 8k = kc. (2)
Вычтем из второго уравнения первое.
6c + 7k = 0 c = -7k/6. Подставим это значение в (1).
(-56k/6) + k = -7k²/6 -50k/6 = -7k²/6 k = 50/7, c = -50/6.
Получаем уравнение заданной плоскости:
(x/(50/7)) + (y/(50/7)) - (z/(50/6)) = 1 "в отрезках"
7x + 7y - 6z - 50 = 0 общее.