Задание 1 Градусная мера угла AOB равна 1 радиану. Найдите длину дуги АВ. Дескриптор: Обучающийся - применяет определение радианной меры для нахождения длины дуги; - находит длину дуги АВ.
Введем дополнительные обозначения: Пусть окружность касается стороны CD в точке К, ОЕ1 и ОЕ2 - высоты трапеции АОQD a) по условию АВ-диаметр окружности, значит АО=ОВ=R ABCD - равнобедренная трапеция, следовательно ∠ВАD=∠CDA и AB=CD=2R Если Q - середина CD, то ОQ - средняя линия трапеции. Следовательно AO=OB=CQ=QD=R Также АО=ОН=R, то есть ΔАОН-равнобедренный, значит ∠ВАD=∠OHA При этом ∠ВАD=∠CDA, следовательно ∠OHA=∠CDA, значит эти углы соответственные при параллельных прямых ОН и DQ и секущей АD. Итак, ОН=QD и ОН || QD, следовательно DQOH-параллелограмм.
б) ∠ВАD=∠OHA=60° ∠АОН=180°-(∠ВАD+∠OHA)=180°-(60°+60°)=60° - ΔАОН - равносторонний, следовательно АН=R ∠ABC=∠BCD=180°-60°=120° Если окружность касается CD, то ∠OKC=90° и ОК=R Сумма всех углов в четырехугольнике равна 360° ∠ВОК=360°-(∠ОВС+∠OKC+∠DCK)=360°-(120°+90°+120°)=30° Если ОQ -средняя линия трапеции, то OQ || AD, следовательно ∠BAD=∠BOQ=60° ∠KOQ=∠BOQ-∠ВОК=60°-30°=30° ΔOQK -прямоугольный с прямым углом OKQ OQ=HD- так как DQOH-параллелограмм средняя линия трапеции =(а+в)/2
Розв'язання: Проведемо медіану до основи BC у точку K, тоді CK = BK =
= BC : 2 = 10 : 2 = 5 см.Нехай медіани AK і BM - перетинаються в
точці O.За теоремою про медіану, медіани точкою перетину діляться у відношенні 2 : 1, рахуючи від вершини кута.Введемо коефіціент пропорційності y, тоді BO = 2y,MO = y, так як медіани AK і BM - перетинаються в точці O.
BM = BO + MO;
8 = 2y + y;
8 = 3y;
y = ;
BO = 2y = 2 * ; MO = y = ;
За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, тоді за теоремою Піфагора: ;
Введемо коефіціент пропорційності x, тоді OK = x, AO = 2x за теоремою про медіану, так як медіани AK і BM - перетинаються в точці O.
AK = OK + AO;
AK = x + 2x = 3x = 3*OK = ;
За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, тоді за теоремою Піфагора:
Пусть окружность касается стороны CD в точке К, ОЕ1 и ОЕ2 - высоты трапеции АОQD
a) по условию АВ-диаметр окружности, значит АО=ОВ=R
ABCD - равнобедренная трапеция, следовательно ∠ВАD=∠CDA и AB=CD=2R
Если Q - середина CD, то ОQ - средняя линия трапеции. Следовательно AO=OB=CQ=QD=R
Также АО=ОН=R, то есть ΔАОН-равнобедренный, значит
∠ВАD=∠OHA
При этом ∠ВАD=∠CDA, следовательно ∠OHA=∠CDA, значит эти углы соответственные при параллельных прямых ОН и DQ и секущей АD.
Итак, ОН=QD и ОН || QD, следовательно DQOH-параллелограмм.
б) ∠ВАD=∠OHA=60°
∠АОН=180°-(∠ВАD+∠OHA)=180°-(60°+60°)=60° - ΔАОН - равносторонний, следовательно АН=R
∠ABC=∠BCD=180°-60°=120°
Если окружность касается CD, то ∠OKC=90° и ОК=R
Сумма всех углов в четырехугольнике равна 360°
∠ВОК=360°-(∠ОВС+∠OKC+∠DCK)=360°-(120°+90°+120°)=30°
Если ОQ -средняя линия трапеции, то OQ || AD, следовательно
∠BAD=∠BOQ=60°
∠KOQ=∠BOQ-∠ВОК=60°-30°=30°
ΔOQK -прямоугольный с прямым углом OKQ
OQ=HD- так как DQOH-параллелограмм
средняя линия трапеции =(а+в)/2
AB = AC =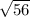 см
см
Объяснение:
Дано:
AC = AB, BC = 10 см, BM = 8 см, CM = MA
Знайти: AC,AB - ?
Розв'язання: Проведемо медіану до основи BC у точку K, тоді CK = BK =
= BC : 2 = 10 : 2 = 5 см.Нехай медіани AK і BM - перетинаються в
точці O.За теоремою про медіану, медіани точкою перетину діляться у відношенні 2 : 1, рахуючи від вершини кута.Введемо коефіціент пропорційності y, тоді BO = 2y,MO = y, так як медіани AK і BM - перетинаються в точці O.
BM = BO + MO;
8 = 2y + y;
8 = 3y;
y =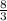 ;
;
BO = 2y = 2 *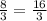 ; MO = y =
; MO = y = 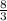 ;
;
За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, тоді за теоремою Піфагора: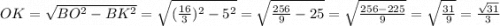 ;
;
Введемо коефіціент пропорційності x, тоді OK = x, AO = 2x за теоремою про медіану, так як медіани AK і BM - перетинаються в точці O.
AK = OK + AO;
AK = x + 2x = 3x = 3*OK =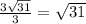 ;
;
За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, тоді за теоремою Піфагора:
Так як AB = BC за умовою, то AB = AC =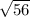 см.
см.