Задача 2

Нарисуйте схему и рассчитайте

а) под каким углом касательные нарисованы от концов хорды с длиной, равной радиусу

пересекаются?

б) Прямая AB касается точки B с окружностью радиуса r, центром которой является точка O. если

Если 0 AOB = ∠ 30, r = 4 см, найдите длину AO.

в) Прямая AB касается точки B с окружностью радиуса r, центром которой является точка O. если

∠ AОB = 600

Если r = 12 см, найдите длину УСОЛЯЮ

ответ: 46°

Объяснение:  Отметим на рисунке  дополнения согласно условию задачи и рассмотрим треугольник АВС. По условию ВК - биссектриса, Она же - медиана, т.к. СК=1/2 АС (дано). Если биссектриса угла треугольника совпадает с медианой из той же вершины, этот треугольник - равнобедренный с основанием АС. В равнобедренном треугольнике углы при его основании равны. =>

Угол АСВ=углу А. ⇒ ∠ А=2 ∠ ВСМ, и угол 2 (угол ВСМ)=1/2 ∠ А. По условию ∠1+∠2=69°. Поэтому х°+1/2х°=69° => 1,5х°=69°=>

х°=46°

1. 37

2. 41

3. 15

4. 24

5. CD = 12; BD = 5; BC = 13; AD = 13; AO = 6,5; DO = 6,5; BO = 6,5; CO = 6,5

Объяснение:

Сумма квадратных катетов равна квадратной гипотенузе.

1. 12^2 + 35^2 = 144 + 1225 = 1369

= 37

ответ: 37

2. 40^2 + 9^2 = 1600 + 81 = 1681

= 41

ответ: 41

3. 8^2 + x^2 = 17^2

64 + x^2 = 289

x^2 = 289 - 64

x^2 = 225

x =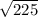

x = 15

ответ: 15

4. 7^2 + x^2 = 25^2

49 + x^2 = 625

x^2 = 625 - 49

x^2 = 576

x =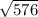

x = 24

ответ: 24

5. BC = 12^2 + 5^2 = 144 + 25 = 169

= 13

Так как ABCD - параллелограмм, то CD = AB = 12; BD = AC = 5; AD = BC = 13.

AO = DO = BO = CO = 13 / 2 = 6,5

ответ: CD = 12; BD = 5; BC = 13; AD = 13; AO = 6,5; DO = 6,5; BO = 6,5; CO = 6,5