2. Углы в 65° равны как накрест лежащие, следовательно AB || CD, следовательно угол а равен 85° как соответственный.
3. <BAC + <AMK = 180°, а они односторонние углы, следовательно MK || AC, следовательно <MKB = <ACB, следовательно <MKB - <ACB = 0.
4. Пусть x - коэффициент пропорциональности, следовательно углы будут 2x и 7x.
Сумма односторонних углов при параллельных прямых равна 180°, следовательно составляем уравнение.
2x + 7x = 180
9x = 180
x = 20
Меньший угол будет равен 2 × 20 = 40°.
5. (см. рисунок)
<CBM = <BMA как накрест лежащие (т. к. BC || AD по условию).
<ABM = <BMA, следовательно треугольник ABM - равнобедренный.
а) BC1 || AD1, поэтому угол между прямыми AB1 и BC1 равен углу между AB1 и AD1.
ребро куба равно а, поэтому (так как грани куба - квадраты), то AB1=AD1=B1D1, а значит треугольник AB1D1 - правильный(равносторонний),
углы равностороннего треугольника равны 60 градусов,
значит искомый угол между прямыми AB1 и BC1 равен 60 градусов
б) так как В1С1 - перпендикуляр с точки С1 на грань АА1В1В, то угол между прямой AC1 и гранью AA1B1B равен углу В1АС1
(треугольник АВ1С1 - прямоугольным с прямым углом АВ1С1)
по свойству диагонали квадрата
по свойству диагонали куба
угол В1АС1 равен arccos корень(2/3)т.е.
угол между прямой AC1 и гранью AA1B1B равен arccos корень(2/3) градусов
2. Углы в 65° равны как накрест лежащие, следовательно AB || CD, следовательно угол а равен 85° как соответственный.
3. <BAC + <AMK = 180°, а они односторонние углы, следовательно MK || AC, следовательно <MKB = <ACB, следовательно <MKB - <ACB = 0.
4. Пусть x - коэффициент пропорциональности, следовательно углы будут 2x и 7x.
Сумма односторонних углов при параллельных прямых равна 180°, следовательно составляем уравнение.
2x + 7x = 180
9x = 180
x = 20
Меньший угол будет равен 2 × 20 = 40°.
5. (см. рисунок)
<CBM = <BMA как накрест лежащие (т. к. BC || AD по условию).
<ABM = <BMA, следовательно треугольник ABM - равнобедренный.
а) BC1 || AD1, поэтому угол между прямыми AB1 и BC1 равен углу между AB1 и AD1.
ребро куба равно а, поэтому (так как грани куба - квадраты), то AB1=AD1=B1D1, а значит треугольник AB1D1 - правильный(равносторонний),
углы равностороннего треугольника равны 60 градусов,
значит искомый угол между прямыми AB1 и BC1 равен 60 градусов
б) так как В1С1 - перпендикуляр с точки С1 на грань АА1В1В, то угол между прямой AC1 и гранью AA1B1B равен углу В1АС1
(треугольник АВ1С1 - прямоугольным с прямым углом АВ1С1)
по свойству диагонали квадрата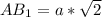
по свойству диагонали куба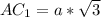
угол В1АС1 равен arccos корень(2/3)т.е.
угол между прямой AC1 и гранью AA1B1B равен arccos корень(2/3) градусов