З точки М що лежить поза колом, проведено до кола дві дотичні МА і МВ де А і В точки дотику. кут МВА = 60°. Знайдіть відстань від точки М до центра кола, якщо радіус кола дорівнює 10 см
1)так, тому що в колі до центра з кожної точки одна й та сама відстань(так, потому что в кругу к центру с каждой точки одно и то же расстояние)
2)ні, пряма має бескінечну кількісьть семетрій(прямая имеет бесконечное число осей симметрии)
3)так кожна вісь семетрична(верно, каждая ось симметрии любого правильного многоугольника с нечетным числом сторон проходит через вершину и середину противоположной стороны.)
4)ні, центр симетрії квадрата є точка перетинаються діагональю.(центр симметрии квадрата является точка пересечения диагоналей.)
Угол А будет равен арксинусу этого числа 59,95 можно округлить до 60°.
5) В треугольнике угол MNO будет равен 30°, поскольку в треугольник MNK прямоугольный. Гипотенуза MN будет равно 6, так как катет МО лежит на против угла в 30°, а значит он равен половине гипотенузы. Катет NO находим по теореме Пифагора . В прямоугольном треугольнике NOK катет NO лежит на против угла в 30°, значит он равен половине гипотенузы, следовательно гипотенуза NK = 10,4. Катет ОК находим по теореме Пифагора ОК = 9,0066 округлим до 9. МК = МО + ОК = 12.
2 Вариант
1) Сумма всех углов прямоугольного треугольника равна 180°, следовательно угол К будет равен К = 180 - 90 - 72 = 18°.
2) Катет ВС лежит на против угла А, который равен 30°, следовательно катет равен половине гипотенузы 15 см.
3) Катет XZ лежит на против угла в 30° он равен половине гипотенузы, следовательно гипотенуза XY = 2*XZ = 24.
4) Находим катет АС по теореме Пифагора. АС = 36,4. Находим синус угла В, sin(B) = 36,4/42 = 0,8666. Угол В будет равен арксинусу этого числа. Угол В равен 60,07° можно округлить до 60°
5) В прямоугольном треугольнике АВС, катет АС лежит на против угла в 30°, следовательно он равен половине гипотенузы АВ, катет АС = 40 см. В треугольнике МСВ угол МСВ равен 60°, поскольку в этом треугольнике угол СМВ прямой. Следовательно угол АСМ = 90-60 = 30°. В треугольнике АСМ катет АМ лежит на против угла в 30° и он равен половине от гипотенузы АС, следовательно катет АМ = 20см.
Відповідь:
1)так(да); 2)ні(нет); 3)так(да); 4)ні(нет).
Пояснення:
1)так, тому що в колі до центра з кожної точки одна й та сама відстань(так, потому что в кругу к центру с каждой точки одно и то же расстояние)
2)ні, пряма має бескінечну кількісьть семетрій(прямая имеет бесконечное число осей симметрии)
3)так кожна вісь семетрична(верно, каждая ось симметрии любого правильного многоугольника с нечетным числом сторон проходит через вершину и середину противоположной стороны.)
4)ні, центр симетрії квадрата є точка перетинаються діагональю.(центр симметрии квадрата является точка пересечения диагоналей.)
1 вариант
1) Сумма всех углов прямоугольного треугольника 180°, следовательно угол А = 180-90-43 = 47°
2) Катет лежащий на против угла в 30° градусов равен половине гипотенузы СВ = АВ/2 = 12см
3) Катет лежащий на против угла в 30° градусов равен половине гипотенузы угол М = 30°, следовательно KL = КМ/2 = 9 см
4) Находим катет ВС по теореме Пифагора
Находим синус угла А, sin(A) = 13,85/16 = 0,865625
Угол А будет равен арксинусу этого числа 59,95 можно округлить до 60°.
5) В треугольнике угол MNO будет равен 30°, поскольку в треугольник MNK прямоугольный. Гипотенуза MN будет равно 6, так как катет МО лежит на против угла в 30°, а значит он равен половине гипотенузы. Катет NO находим по теореме Пифагора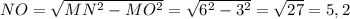
. В прямоугольном треугольнике NOK катет NO лежит на против угла в 30°, значит он равен половине гипотенузы, следовательно гипотенуза NK = 10,4. Катет ОК находим по теореме Пифагора ОК = 9,0066 округлим до 9. МК = МО + ОК = 12.
2 Вариант
1) Сумма всех углов прямоугольного треугольника равна 180°, следовательно угол К будет равен К = 180 - 90 - 72 = 18°.
2) Катет ВС лежит на против угла А, который равен 30°, следовательно катет равен половине гипотенузы 15 см.
3) Катет XZ лежит на против угла в 30° он равен половине гипотенузы, следовательно гипотенуза XY = 2*XZ = 24.
4) Находим катет АС по теореме Пифагора. АС = 36,4. Находим синус угла В, sin(B) = 36,4/42 = 0,8666. Угол В будет равен арксинусу этого числа. Угол В равен 60,07° можно округлить до 60°
5) В прямоугольном треугольнике АВС, катет АС лежит на против угла в 30°, следовательно он равен половине гипотенузы АВ, катет АС = 40 см. В треугольнике МСВ угол МСВ равен 60°, поскольку в этом треугольнике угол СМВ прямой. Следовательно угол АСМ = 90-60 = 30°. В треугольнике АСМ катет АМ лежит на против угла в 30° и он равен половине от гипотенузы АС, следовательно катет АМ = 20см.