Розв'язання: Проведемо медіану до основи BC у точку K, тоді CK = BK =
= BC : 2 = 10 : 2 = 5 см.Нехай медіани AK і BM - перетинаються в
точці O.За теоремою про медіану, медіани точкою перетину діляться у відношенні 2 : 1, рахуючи від вершини кута.Введемо коефіціент пропорційності y, тоді BO = 2y,MO = y, так як медіани AK і BM - перетинаються в точці O.
BM = BO + MO;
8 = 2y + y;
8 = 3y;
y = ;
BO = 2y = 2 * ; MO = y = ;
За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, тоді за теоремою Піфагора: ;
Введемо коефіціент пропорційності x, тоді OK = x, AO = 2x за теоремою про медіану, так як медіани AK і BM - перетинаються в точці O.
AK = OK + AO;
AK = x + 2x = 3x = 3*OK = ;
За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, тоді за теоремою Піфагора:
В треугольнике ABC DN - средняя линия по определению. Значит, по свойству средней линии ND параллельна AB.Отсюда следует параллельность ND и KB,так как KB = 1/2 AB. Имеем также, что ND = 1/2*AB = 1/2*10 = 5 (см). Так как по условию задачи точка K - середина отрезка AB, то KB = 1/2*10 = 5 (см). Аналогично рассуждая,доказываем, что КD - средняя линия треугольника ABC,что KD параллельна NB, что KD = 1/2*BC = 5 (см) и что BN = 5 см. Рассмотрим четырехугольник KBND. В нём ND параллельна KB и KD параллельна BN (по ранее доказанному). Также мы имеем, что NB = KD = 5 см и что KB = DN = 5 см. Значит, по определению данный четырехугольник - параллелограмм. А следуя из того, что NB = KD = KB = DN = 5 см, то получаем, что KBND - ромб. Найдем периметр данной фигуры. P = 5*4 = 20 (см). ответ: ромб; 20 см
AB = AC =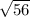 см
см
Объяснение:
Дано:
AC = AB, BC = 10 см, BM = 8 см, CM = MA
Знайти: AC,AB - ?
Розв'язання: Проведемо медіану до основи BC у точку K, тоді CK = BK =
= BC : 2 = 10 : 2 = 5 см.Нехай медіани AK і BM - перетинаються в
точці O.За теоремою про медіану, медіани точкою перетину діляться у відношенні 2 : 1, рахуючи від вершини кута.Введемо коефіціент пропорційності y, тоді BO = 2y,MO = y, так як медіани AK і BM - перетинаються в точці O.
BM = BO + MO;
8 = 2y + y;
8 = 3y;
y =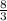 ;
;
BO = 2y = 2 *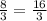 ; MO = y =
; MO = y = 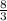 ;
;
За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, тоді за теоремою Піфагора: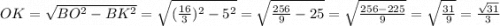 ;
;
Введемо коефіціент пропорційності x, тоді OK = x, AO = 2x за теоремою про медіану, так як медіани AK і BM - перетинаються в точці O.
AK = OK + AO;
AK = x + 2x = 3x = 3*OK =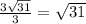 ;
;
За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, тоді за теоремою Піфагора:
Так як AB = BC за умовою, то AB = AC =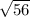 см.
см.
Так как по условию задачи точка K - середина отрезка AB, то KB = 1/2*10 = 5 (см).
Аналогично рассуждая,доказываем, что КD - средняя линия треугольника ABC,что KD параллельна NB, что KD = 1/2*BC = 5 (см) и что BN = 5 см.
Рассмотрим четырехугольник KBND. В нём ND параллельна KB и KD параллельна BN (по ранее доказанному). Также мы имеем, что NB = KD = 5 см и что KB = DN = 5 см. Значит, по определению данный четырехугольник - параллелограмм. А следуя из того, что NB = KD = KB = DN = 5 см, то получаем, что KBND - ромб.
Найдем периметр данной фигуры.
P = 5*4 = 20 (см).
ответ: ромб; 20 см