Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя неравная им сторона — основанием.
АВ=ВС=21см
Рассмотрим прямоугольный ΔAВD(∠D=90°)
По теореме Пифагора найдём катет AD:
В равнобедренном треугольнике высота, проведенная к основанию, является так же и медианой: AD=DC
AC=2*AD=2*14=28 cм
Косинус угла – это отношение прилежащего (близкого) катета к гипотенузе:
По таблице косинусов находим значение угла А:
∠ А ≅ 48°
В равнобедренном треугольнике углы при основании равны.
АС=28 см
∠А=48°, ∠С=48°, ∠В=84°
Объяснение:
Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя неравная им сторона — основанием.АВ=ВС=21см
Рассмотрим прямоугольный ΔAВD(∠D=90°)
По теореме Пифагора найдём катет AD:
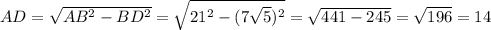
В равнобедренном треугольнике высота, проведенная к основанию, является так же и медианой: AD=DCAC=2*AD=2*14=28 cм
Косинус угла – это отношение прилежащего (близкого) катета к гипотенузе:По таблице косинусов находим значение угла А:
∠ А ≅ 48°
В равнобедренном треугольнике углы при основании равны.∠С = ∠ А ≅ 48°
Сумма углов треугольника равна 180°∠В = 180-∠А-∠С = 180-48-48=84°
Расстояние от точки D до каждой из вершин равностороннего треугольника ABC равно 5 см, AB = 3√3 см.
Найдите расстояние от точки D до плоскости ABC.
4 см
Объяснение:
Проведем DO⊥(АВС). Тогда
DO - искомое расстояние от точки D до плоскости (ABC).
ΔDAO = ΔDBO = ΔDCO по гипотенузе и катету (DA = DB = DC по условию, DO - общий катет), тогда
АО = ВО = СО, то есть, точка О равноудалена от вершин треугольника АВС, значит О - центр описанной окружности.
Радиус окружности, описанной около правильного треугольника:
ΔDAO: ∠DOA = 90°, по теореме Пифагора