Вычислите длину окружности заданной уравнением $x { - 4 + y { - 2 \sqrt{5y = 0} }^{2} }^{2}$

Question

Геометрия: Вычислите длину окружности заданной уравнением ​

ВалерияЛера11111 · Answer

Уравнение окружности имеет вид :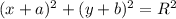 , где (a,b) - координаты центра окружности, а R - это его радиус Постараемся привести наше уравнение к приличному ввиду :Теперь наше уравнение похоже на уравнение окружности, где :Длинна окружности = 2πR = 2 * 3 * 3 = 2 * 9 = 18 ответ : 18...

Вычислите длину окружности заданной уравнением ​

Вычислите длину окружности заданной уравнением $x { - 4 + y { - 2 \sqrt{5y = 0} }^{2} }^{2}$