Все стороны правой прямоугольной пирамиды MAVCD равны 4 см. От середины ребер MA, MB, MC, MD отмечены 4 точки соответственно. Найти отношение площади сечения, проходящего через эти точки, к площади прямоугольника в основании.

Показать ответ

Ответ:

Lyuda56

24.12.2020 09:29

$1) \ x = \sqrt{13} \\2) \ x = \sqrt{21} \\3) x_1 = 7, x_2=x_3 = 7\sqrt{2}$

Объяснение:

Обозначим неизвестные отрезки за x

1) неизвестный отрезок является гипотенузой прямоугольного треугольника:

$x = \sqrt{3^2+2^2} = \sqrt{9+4} = \sqrt{13}$

2) неизвестный отрезок является высотой, проведённой к основанию, в равнобедренном треугольнике. Как известно, высота, проведённая к основанию, в равнобедренном треугольнике является также медианой и биссектрисой. Следовательно неизвестный отрезок делит основание пополам и является катетом в прямоугольном треугольнике с гипотенузой равной 5 и катетом равным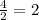 $\frac{4}{2} = 2$ :

$x = \sqrt{5^2 - 2^2} = \sqrt{25 - 4} = \sqrt{21}$

3) Здесь имеется три неизвестных отрезка, два из которых равны.

Начнём с высоты, опять же она проведена к основанию в равнобедренном треугольнике, а значит является и медианой и биссектрисой. А медиана проведённая к гипотенузе в прямоугольном треугольнике равна половине гипотенузы:

$x_1 = \frac{14}{2} = 7$

Нам известно, что оставшиеся неизвестные отрезки являются катетами в прямоугольном треугольнике и что они равны. Нам известна гипотенуза этого треугольника:

$x_2 = x_3,\\\sqrt{x_2^2+x_3^2} = 14 \\\sqrt{2x_2^2} = 14\\x_2\sqrt{2} = 14\\x_2 = \frac{14}{\sqrt{2} } = \frac{14\sqrt{2} }{2} = 7\sqrt{2}$

0,0(0 оценок)

Ответ:

almiradkzbd

03.10.2022 08:01

1. Прямые АВ₁ и DC скрещивающиеся

2. DC ║ (AA₁B₁)

3. АВ₁ ║ (DСС₁)

Объяснение:

Признак скрещивающихся прямых:

если одна прямая лежит в плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то такие прямые скрещивающиеся.

Прямая DC лежит в плоскости (ABC), прямая АВ₁ эту плоскость пересекает в точке А, не лежащей на прямой DC, значит прямые АВ₁ и DC скрещивающиеся по признаку.

Признак параллельности прямой и плоскости:

если прямая, не лежащая в плоскости, параллельна некоторой прямой, лежащей в плоскости, то она параллельна плоскости.

DC и AB параллельны как противоположные стороны параллелограмма, АВ лежит в плоскости (АА₁В₁), значит DC параллельна плоскости (АА₁В₁) по признаку.

Проведем DC₁. Докажем, что АВ₁║DC₁:

AD║BC, AD = BC, BC║B₁C₁, BC = B₁C₁ как противоположные стороны параллелограммов, значит

AD║B₁C₁ и AD = B₁C₁, следовательно AB₁C₁D - параллелограмм.

Тогда АВ₁║DC₁. DC₁ ⊂ (DCC₁), значит АВ₁║(DCC₁) по признаку параллельности прямой и плоскости.