Впсрямоугольной трапеции abcd меньшее основание ad
разно 3, а боковая сторона cd, не перпендикулярная к осно-
ваниям , равна 6. точка e — середина отрезка cd, угол cbe
равен a. найдите площадь трапеции abcd.

Показать ответ

Ответ:

lilyamkrtchyan1

16.02.2021 16:59

S треугольника всегда = высота*основание к которому она проведена разделить это всё на два. (h*осн.)/2

1) высота - 6, основание 12, значит площадь - 12*6/2= 72/2=36 - Б

2)Если в треугольнике есть угол в 30 градусов, то сторона напротив него - в два раза меньше гипотенузы ( стороны напротив прямого=90 угла).

Тут гипотенуза = 12 значит сторона напротив угла равна 12/2 = 6. Чтобы найти вторую сторону используем теорему Пифагора.

a^2+b^2=c^2

где а и б - стороны, а с - гипотенуза. Подставим известное...

6^2+b^2=12^2

36+B^2=144

b^2=144-36

b^2=108

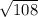
b = $\sqrt{108}$

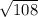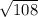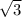Площадь треугольника здесь - 6* $\sqrt{108}$ /2 = 3* $\sqrt{108}$ =18 $\sqrt{3}$ -в

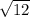3)Опустим высоту. Найдём её тоже через свойство угла в 30 градусов и теорему пифагора. 16-4=12 значит высота $\sqrt{12\\}$ . в итоге.

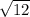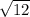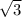площадь= $\sqrt{12}$ *6=6 $\sqrt{12}$ =12 $\sqrt{3}$ - в

4)Наименьшая высота будет опущена к самой большой стороне, запомни. Опустим ее к стороне 20. Через формулы ( набери в инете среднее геометрическое, долго оформлять очень ) найдём, что x=12,8 - кусочек, которой получается в результате деления высотой стороны двадцать, который ближе к стороне 16. Аналогично найдём и кусочек, ближний к стороне 12. y=7,2. Высота равна корню произведения xy= 9,6 - высота - г

0,0(0 оценок)

Ответ:

lllllll47900732

25.12.2021 00:33

Определение: "Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость".

Опустим перпендикуляр С1Н на прямую СD1, лежащую в плоскости А1ВС (это плоскость А1ВСD1, так как секущая плоскость пересекает параллельные плоскости АА1В1В и DD1C1C по параллельным прямым А1В и D1C). Отрезок С1Н перпендикулярен любой прямой, проходящей через точку Н, лежащую в данной плоскости (свойство). Значит <C1HB=90° и искомый угол - это угол С1ВН - угол между наклонной ВС1 м ее проекцией ВН на плоскость А1ВС. В прямоугольном треугольнике С1ВН: синус угла С1ВН - это отношение противолежащего катета С1Н к гипотенузе ВС1.

По Пифагору D1C=√(D1C1²+CC1²) = √(36+64) = 10 ед (так как АВ=D1C1, a AA1=CC1, как боковые ребра параллелепипеда.

Точно так же ВС1=√(ВC²+CC1²) = √(225+64) = 17 ед.

Высота С1Н из прямого угла по ее свойству равна:

С1Н=(С1D1*CC1/D1C = 6*8/10 = 4,8 ед.

Тогда Sinα = C1H/BC1 = 4,8/17 ≈ 0,2823.

α = arcsin0,2823 ≈ 16,4°.