Вправильной треугольной пирамиде плоский угол при вершине равен 30 градусов, а кратчайшее расстояние между боковым ребром и противоположной стороной основания равно 3 см. найдите объём этой пирамиды. (желательно с чертежом)
правильная пирамида - все углы равны и стороны равны.Таким образом, задан тетраэдр.
плоский угол при вершине - угол между двумя ребрами.
Пусть боковая сторона равна а.
Рассмотрим прямоугольный треугольник ABC, образованный боковой стороной тетраэдра, её проекцией на основание и высотой пирамиды.
Ясно, что основание высоты равноудалено от вершин основания, то есть проекция бокового ребра на основание есть радиус R описанной окружности вокруг треугольника со стороной а, т. е. R =;
Заданный отрезок длины 3 является в построенном прямоугольном треугольнике МЕДИАНОЙ, то есть равен половине гипотенузы. А роль гипотенузы играет боковое ребро. Поэтому а = 6
Площадь правильного треугольника со стороной 6 равна = 6^2*√3/4; а всего у нас 4 одинаковых грани, то есть площадь всей поверхности пирамиды равна
Обозначим пирамиду АВСS(смотри рисунок). Пирамида правильная значит в основании лежит правильный треугольник( обозначим его сторону а) и высота ОS пирамиды проецируется в центр основания. Кратчайшее расстояние МК перпендикулярна АS. Из треугольника SВК найдём боковое ребро. Прямоугольные треугольники АМК и АSО подобны по острому углу SАО. Отсюда находим Н. Дальше по теореме Пифагора, из треугольника АSО находим выражение а квадрат. Подставляем найденные значения в известную формулу. ответ на рисунке.
правильная пирамида - все углы равны и стороны равны.Таким образом, задан тетраэдр.
плоский угол при вершине - угол между двумя ребрами.
Пусть боковая сторона равна а.
Рассмотрим прямоугольный треугольник ABC, образованный боковой стороной тетраэдра, её проекцией на основание и высотой пирамиды.
Ясно, что основание высоты равноудалено от вершин основания, то есть проекция бокового ребра на основание есть радиус R описанной окружности вокруг треугольника со стороной а, т. е. R =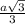
;
Заданный отрезок длины 3 является в построенном прямоугольном треугольнике МЕДИАНОЙ, то есть равен половине гипотенузы. А роль гипотенузы играет боковое ребро. Поэтому а = 6
Площадь правильного треугольника со стороной 6 равна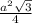
= 
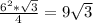6^2*√3/4; а всего у нас 4 одинаковых грани, то есть площадь всей поверхности пирамиды равна
Обозначим пирамиду АВСS(смотри рисунок). Пирамида правильная значит в основании лежит правильный треугольник( обозначим его сторону а) и высота ОS пирамиды проецируется в центр основания. Кратчайшее расстояние МК перпендикулярна АS. Из треугольника SВК найдём боковое ребро. Прямоугольные треугольники АМК и АSО подобны по острому углу SАО. Отсюда находим Н. Дальше по теореме Пифагора, из треугольника АSО находим выражение а квадрат. Подставляем найденные значения в известную формулу. ответ на рисунке.