Восновании пирамиды лежит прямоугольный равнобедренный треугольник с гипотенузой с. каждое ребро пирамиды накланено к плоскости под углом 45°. найдите площадь полной поверхности пирамиды.
Даны два вектора m{-1; 2} и n{4;-x}. Найдите: а) При каких значениях x прямые, содержащие данные векторы, коллинеарны?
б) При каких значениях x прямые, содержащие данные векторы, перпендикулярны?
в) При каких значениях x прямые, содержащие данные векторы, образуют тупой угол?
Решение
а) Два вектора коллинеарные ,если их координаты пропорциональны, значит для m{-1; 2} и n{4;-x} имеем -1:4=2:(-х) , х=8;
б)Вектора перпендикулярны , если их скалярное произведение равно нулю : m*n=-1*4+2*(-х) , -1*4+2*(-х) =0 , x=2;
a) Угол будет тупым , если cos(∠m;n) <0 .Косинус угла между векторами равен скалярному произведению этих векторов, деленному на произведение их длин.
Найдем длины векторов:
Длина вектора |m|=√( (-1)²+2²)=√(1 +4)=√5,
Длина вектора |n|=√( 4²+(-x)²)=√(16+x²),
Скалярное произведение m*n=-1*4+2*(-х)=-4-2x
(-4-2x)/ (√5*√(16+x²))<0/Значение дроби отрицательно , числитель и знаменатель разных знаков. Но √5*√(16+x²)>0 при х≠±4, тогда -4-2х<0 или х>2. Тогда учитывая х≠4 получаем х∈(2;4)∪(4;+∞).
Многогранный угол составлен боковыми сторонами -угольной пирамиды, в основании которой лежит выпуклый -угольник. Рассмотрим одну из таких сторон. Докажем, что (см. рисунок). Тогда и . Вот сейчас будет немного муторно: . Однако , действительно, , что верно, поскольку каждое слагаемое слева (кроме единицы) больше соответствующего слагаемого справа. Поэтому . Теперь спроецировав вершину многогранного угла на плоскость (многоугольник), получим, что сумма плоских углов меньше суммы углов при вершине проекции , которая равна в точности , что и требовалось.
Даны два вектора m{-1; 2} и n{4;-x}. Найдите: а) При каких значениях x прямые, содержащие данные векторы, коллинеарны?
б) При каких значениях x прямые, содержащие данные векторы, перпендикулярны?
в) При каких значениях x прямые, содержащие данные векторы, образуют тупой угол?
Решение
а) Два вектора коллинеарные ,если их координаты пропорциональны, значит для m{-1; 2} и n{4;-x} имеем -1:4=2:(-х) , х=8;
б)Вектора перпендикулярны , если их скалярное произведение равно нулю : m*n=-1*4+2*(-х) , -1*4+2*(-х) =0 , x=2;
a) Угол будет тупым , если cos(∠m;n) <0 .Косинус угла между векторами равен скалярному произведению этих векторов, деленному на произведение их длин.
Найдем длины векторов:
Длина вектора |m|=√( (-1)²+2²)=√(1 +4)=√5,
Длина вектора |n|=√( 4²+(-x)²)=√(16+x²),
Скалярное произведение m*n=-1*4+2*(-х)=-4-2x
(-4-2x)/ (√5*√(16+x²))<0/Значение дроби отрицательно , числитель и знаменатель разных знаков. Но √5*√(16+x²)>0 при х≠±4, тогда -4-2х<0 или х>2. Тогда учитывая х≠4 получаем х∈(2;4)∪(4;+∞).
Многогранный угол составлен боковыми сторонами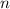 -угольной пирамиды, в основании которой лежит выпуклый
-угольной пирамиды, в основании которой лежит выпуклый 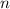 -угольник. Рассмотрим одну из таких сторон. Докажем, что
-угольник. Рассмотрим одну из таких сторон. Докажем, что  (см. рисунок). Тогда
(см. рисунок). Тогда 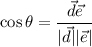 и
и 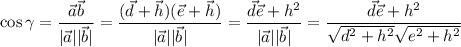 . Вот сейчас будет немного муторно:
. Вот сейчас будет немного муторно: 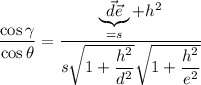 . Однако
. Однако 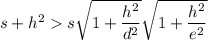 , действительно,
, действительно, 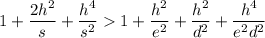 , что верно, поскольку каждое слагаемое слева (кроме единицы) больше соответствующего слагаемого справа. Поэтому
, что верно, поскольку каждое слагаемое слева (кроме единицы) больше соответствующего слагаемого справа. Поэтому 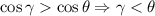 . Теперь спроецировав вершину
. Теперь спроецировав вершину 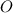 многогранного угла на плоскость (многоугольник), получим, что сумма плоских углов меньше суммы углов при вершине
многогранного угла на плоскость (многоугольник), получим, что сумма плоских углов меньше суммы углов при вершине 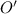 проекции
проекции 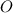 , которая равна в точности
, которая равна в точности 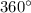 , что и требовалось.
, что и требовалось.