Внешние углы треугольника относятся как 4: 5: 6.найти отношение внутренних углов треугольника. ​

68 см

Объяснение:

1) Знайдемо іншу сторону прямокутника

Діагональ прямокутника ділить прямокутник на два прямокутних трикутника, у яких гіпотенуза такого трикутника це  діагональ  прямокутника, а сторони прямокутника є катетами такого трикутника

За теоремою Піфагора квадрат гіпотенузи дорівнює сумі квадратів катетів ⇒квадрат відомого катета дорівнює різниці квадрата гіпотенузи та квадрата невідомого катета, який і є другою стороною трикутника. тому:

26²-10²=676-100=576, √576=24 (см) - інша сторона прямокутника

2)Знайдемо периметр прямокутника

У прямокутника   протилежні сторони рівні, тому

Р=2(а+b), де а та b - сторони прямокутника, тому

Р=2*(24+10)=68 (см)

Объяснение:

Так как призма прямая, то длина ее высоты равна длине бокового ребра призмы.

Площадь боковой поверхности призмы равна:

S(бок) = S(AA₁C₁C) + S(BB₁C₁C) + S(AA₁B₁B)

Найдем боковую сторону равнобедренного треугольника в основании призмы:

Проведем высоту BH равнобедренного треугольника ABC с основанием AC.

По свойству высоты равнобедренного треугольника, проведенной к основанию, BH будет медианой, поэтому AH = CH = AC/2 = 4 см

По теореме Пифагора найдем AB:

AB =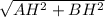 = = 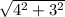5

S(AA₁C₁C) = AA₁ * AC = 6 * 8 = 48 см²

S(BB₁C₁C) = BB₁ * BC = 6 * 5 = 30 см²

S(AA₁B₁B) = AB * AA₁ = 5 * 6 = 30 см²

S(бок) = 48 см² + 30 см² + 30 см² = 108 см²