Виконали паралельне перенесення прямої 2х+у-8=0 . Запишіть рівняння прямої яку при цьому отрималм, якщо вона проходить через точку А (5; 1)
выполнили параллельный перенос прямой 2х + у-8 = 0. Запишите уравнение прямой которую при этом получили, если она проходит через точку А (5; 1)
хелп ми
Т.к. пирамида правильная, значит в основании лежит равносторонний треугольник АВС, в котором высота является и медианой и биссектрисой. Точкой Р обозначим точку, в которую опущена высота ВР этого треугольника. Высота делит АВС на два равных прямоугольных треугольника АВР и ВРС.
Пусть АВ=х - сторона основания пирамиды, тогда РС=х/2.
Тогда по теореме Пифагора х^2=(x/2)^2+3^2
или x^2=1/4*x^2+9. Отсюда находим х=корень из 12.
Тогда площадь равностороннего треугольника Sabc=1/2*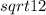 *
*![sqrt{12}[/tex*sin60=3[tex]sqrt{3}](/tpl/images/0167/6314/05f01.png)
Периметр треугольника Р=3*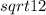
Тогда площадь полной поверхности пирамиды есть S=1/2PL+Sabc, где L - апофема
S=1/2*3*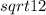 *4+3*
*4+3*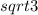 =15
=15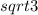
P_MNK=a+b+c=36 дм,
P_MNL = a+l+c/2=24 дм,
P_MKL = b+l+c/2=20 дм.
Сложим второе и третье уравнения.
a+l+c/2+b+l+c/2=24 дм + 20 дм
a+b+c+2l=44 дм.
Отсюда l = (44 дм - (a+b+c))/2 = (44-36)/2 дм = 4 дм.
Задача 2.
∠C=74°. Пусть ∠A=2α, ∠B=2β. Тогда ∠B=180°-∠C-∠A=180°-74°-2α=106°-2α=2β. Отсюда β=(106°-2α)/2=53°-α.
Пусть искомый угол γ. Тогда α+β+γ=180°. γ=180°-(α+β)=180°-(α+53°-α)=127°.
Задача 3.
x+5=x^2
x^2-x-5=0
В любом случае это уравнение имеет 2 корня, поскольку это уравнение второй степени от одной переменной. Вопрос в том, действительные ли эти корни и являются ли они кратными. Корни квадратного уравнения являются комплексными, если дискриминант отрицателен. Корни квадратного уравнения являются кратными, если дискриминант равен 0 - в этом случае квадратное уравнение имеет два одинаковых корня.
D=(-1)^2-4*1*(-5)=21 > 0 - уравнение имеет два различных действительных корня.