Верно ли утверждение? а) Длина перпендикуляра, опущенного из данной точки к прямой, называется расстоянием от точки до прямой;
б) Конец наклонной, лежащий вне данной прямой, называется основанием наклонной;
в) Если прямая параллельна данной прямой, то все ее точки находятся на одинаковом расстоянии;
г) Если к прямой проведены две наклонные, то их проекции на прямую равны.
д) Конец отрезка, являющегося перпендикуляром к прямой, лежащего в ней, называется
основанием перпендикуляра;
е) Отрезок, соединяющий основание наклонной с данной точкой, не лежащей на прямой, называется проекцией наклонной;
ж) Проекцией перпендикуляра является точка, а наклонной – отрезок;
з) Если две наклонные имеют равные проекции, то они сами равны

быстрей

Трапеция ABCD вписана в окружность (AD II BC), AB=13, BC=7, периметр 50. Найти:   1. CD и AD  ;  2.среднюю линию трапеции  ;  3. Площадь трапеции  ;  4. tg∠BAD  ;   5.cos ∠BCD  ;  6.AC  ;  7.радиус вписанной окружности  ;  8.радиус описанной окружности.

Объяснение:

1) Описать окружность можно только около равнобедренной трапеции ⇒ CD=13 , Тогда AD=50-(2*13+7)=17.

2)Средняя линия равна полусумме оснований :  .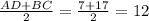

3) S (трапеции) =1/2*h*(a+b)  .Отложим от точки D отрезок DK=BC. Тогда  S (трапеции) =S (ΔАВК) , т.к высоты этих фигур равны .

Пусть ВН⊥АD,  АН=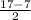   = 5 . Из ΔАВН , по т. Пифагора

ВН=√(13²-5²)=  √( (13+5)(13-5))=√(18*8)=12 .

S (трапеции)=1/2*12*(17+7)=144 (ед²).

4) ΔАВН-прямоугольный, tg∠BAD=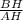  , tg∠BAD=  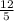, tg∠BAD=2,4 .

5) cos∠BCD= cos∠ABC, тк углы при основании равны.

cos∠ABC=cos(90°+∠АВН) =( по формулам приведения)=- sin∠ABН

Из ΔАВН,  sin∠ABН =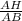  , sin∠ABН = 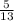 . Получаем  cos∠BCD=-  .

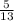6) ΔАВС , по т. косинусов АС²=АВ²+ВС²-2*АВ*ВС*cos∠ABC,

AC²=169+49-2*13*7*( -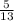  ) , AC²=218+70 ,  AC²=288 , AC=12√2.

7) Из формулы S=1/2*P*r , r=(2*S)/P . r=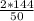  ,  r =5,76

8) Радиус описанной окружности для трапеции совпадает с радиусом описанной окружности для ΔАВС. Найдем R для ΔАВC по т. синусов

=2R ,   =2R .

sin∠ABC=sin(90+∠ABH)=( по формулам приведения) =сos∠ABH.

ΔABH , сos∠ABH=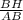  , сos∠ABH=  .Поэтому   sin∠ABC=  .

2R =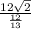   , R=6,5√2 .

Объяснение:

сумма углов треугольника равна 180 градусам сл. -но. угол

В = 180-а-с

В=180-35-45=100

ответ: угол В равен 100 градусам

6)угол а и d - смежные

По теореме смежные углы рвны сл. -но.

угол а = 40 градусам

сумма углов треугольника равна 180 градусам, значит

В=180-А-С=180-40-105=35

ответ: А=40, В=35

9)угол С - внешний

по теореме внешний угол треугольника равен сумме двух углов треугольника не смежных с ним.

Сумма углов треугольника равна 180 градусам сл. -но

С=180-125= 55

этот треугольник равнобедренный, а у равнобедренного треугольника углы при основании равны, значит С=А=55

В=180-55-55=70

ответ А=55 В=70 С=55