Вединичном кубе найдите расстояние от точки а до плоскости а1вс1

Сумма углов треугольника равна 180 градусов. Если углы треугольника относятся как 5 : 6 : 7, то это значит, что первый угол содержит 5 частей, второй - 6 таких же частей, а третий 7 таких же частей градусных мер угла.

Пусть одна часть угла равна х градусов, тогда первый угол треугольника равен 5х градусов, второй угол равен 6х градусов, а третий угол - 7х градусов. По условию задачи известно, что сумма углов треугольника равна (5х + 6х + 7х) градусов или 180°. Составим уравнение и решим его.

5х + 6х + 7х = 180;

18х = 180;

х = 180 : 18;

х = 10° - градусная мера одной части;

5х = 10° * 5 = 50° - первый угол;

6х = 10° * 6 = 60° - второй угол;

7х = 10° * 7 = 70° - третий угол.

Все углы треугольника острые, значит, этот треугольник будет остроугольным.

ответ. 50°, 60°, 70°

Объяснение:

a = 5 см,

b = 4 см,

c = 7 см.

Найти R.

Запишем теорему синусов:

числитель и знаменатель дроби слева последнего равенства домножим на (b·c).

С учётом того, что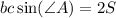 , где S - площадь данного в условии треугольника, имеем

Площадь треугольника можно найти по формуле Герона:

, где

Найдем, сначала, площадь треугольника.

p = (5+4+7)/2 = (9+7)/2 = 16/2 = 8 см.

S = √(8·(8-5)·(8-4)·(8-7)) = √(8·3·4·1) = 4·(√6) см²

Теперь найдем радиус описанной окружности.

R = 5·4·7/(4·4·(√6)) = 5·7/(4·(√6)) = 35·(√6)/(4·6) = 35·(√6)/24 см.

Теперь найдём длину окружности, описанной около данного треугольника.

L = 2πR = 2π·35·(√6)/24 см = π·35·(√6)/12 см.