В треугольной пирамиде SABC известны боковые рёбра: SA = SB = 7, SC = 5. Основанием высоты этой пирамиды является середина медианы CM треугольника ABC. Эта высота равна 4. Докажите, что треугольник ABC равнобедренный.

Показать ответ

Ответ:

semyanivskyilly

29.07.2022 22:55

Случай 1 : Площадь бо́льшего треугольника равна 8 (ед²).Отношение сходственных сторон подобных треугольников равно коэффициенту подобия.

Пусть S₁ - это площадь бо́льшего треугольника, а S₂ - площадь меньшего треугольника.

Пусть k > 1 (это значит, что в числителе будет стоять бо́льший треугольник).

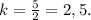
$k = \frac{5}{2} = 2,5.$

Площади подобных треугольников относятся как квадрат коэффициента подобия.

Отсюда -

$\frac{S_{1} }{S_{2} } = k^{2} \\\\\frac{8}{S_{2} } = 2,5^{2} \\\\\frac{8}{S_{2} } = 6,25\\\\S_{2} = \frac{8}{6,25} \\\\\boxed{S_{2} = 1,28}$

1,28 (ед²).

- - -

Случай 2 - Площадь меньшего треугольника равна 8 (ед²).

В этом случае наоборот k < 1 (в числителе будет стоять меньший треугольник).

S₁ - площадь бо́льшего треугольника, S₂ - площадь меньшего треугольника

Тогда -

$k = \frac{2}{5} = 0,4.$

$\frac{S_{2} }{S_{1} } = k^{2}\\\\\frac{8 }{S_{1} } = 0,4^{2}\\\\\frac{8 }{S_{1} } = 0,16\\\\S_{1} = \frac{8}{0,16}\\\\\boxed{S_{1} = 50}$

50 (ед²).

0,0(0 оценок)

Ответ:

nazarzadorozhny

07.06.2021 23:19

Сторона правильної чотирикутної піраміди дорівнює а , а її діагональний переріз – рівносторонній трикутник. Знайдіть об’єм піраміди. 2. Висота правильної чотирикутної піраміди дорівнює 12 см, а апофема – 15 см. Обчисліть площу бічної поверхні піраміди. 3. Сторона основи правильної трикутної піраміди дорівнює 6 см, а висота піраміди - см. Знайдіть площу бічної поверхні піраміди. 4. Сторона основи правильної трикутної піраміди дорівнює 8 см, а бічна грань нахилена до площини основи під кутом 300. Знайдіть площу повної поверхні піраміди. 5. Основа піраміди – трикутник зі сторонами 13 см, 14 см і 15 см. Знайдіть площу перерізу, який проходить паралельно площині основи і ділить висоту піраміди у відношенні 1:2. Рахуючи від вершини піраміди. Знайдіть об‘єм правильної чотирикутної піраміди, сторона основи якої дорівнює 6 см, а діагональний переріз є рівностороннім трикутником

0,0(0 оценок)

Популярные вопросы: Геометрия