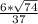В треугольнике АВС угол А= альфа >90, угол В=бетта, высота СD равна h.
а) Найдите сторону АВ и радиус R описанной окружности
б) Вычислите значение R, если альфа=135, h=3см, бетта=30
2. Хорда окружности равна альфа и стягивает дугу в 60 градусов. Найдите: а) длину дуги б) площадь сектора, ограниченного этой дугой и двумя радиусами.

В обеих задачах один из углов в треугольнике = 120°. Этот угол не может быть углом при основании равнобедренного Δ, так как эти углы должны быть равными, и их сумма будет равна 240°, что больше, чем 180°.
 Значит угол в 120° - это угол при вершине.
Углы при основании будут равны (180°-120°):3=30°
1) Опустим высоту из вершины А на бок. сторону ВС (АС - основание равнобедренного ΔАВС), получим точку Н. Она будет лежать на продолжении стороны ВС, т.к. ∠В=120° - тупой.
Рассм. ΔАНС: ∠АНС=90°, ∠АСН=30°  ⇒  АН - катет, лежащий против угла в 30°, равен половине гипотенузы. Гипотенузой является АС=18 см.
АН=18:2=9 (см)

2) В этой задаче всё аналогично, чертёж такой же, только известно не АС, а АВ=ВС=14.
Чтобы найти высоту АН, как катет, лежащий против угла в 30° в ΔАНС, надо вычислить длину основания АС в равнобедренном ΔАВС
 ( АС является   гипотенузой в ΔАНС) .
Теорема косинусов:
АС²=АВ²+ВС²-2·АВ·ВС·сos120°=14²+14²-2·14·14·cos(90°+30°)=
       =2·14²-2·14²·(-cos30°)=2·14²·(1+√3/2)=2·14²·(2+√2)/2=14²·(2+√3)

Объяснение:

Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.

1) прямая DC1 и плоскость A1B1C1

DD1 ⊥ (A1B1C1) ⇒ DD1 ⊥ D1C1 ⇒ D1C1  - проекция прямой DC1 на плоскость A1B1C1, а ∠DС1D1 - искомый угол.

Рассмотрим ΔDС1D1 (∠D1=90°):  

D1C=A1B1=AB=5

DD1=AA1=12

tg ∠DС1D1 = D1D1/C1D1 = 12/5

∠DС1D1 = arctg (12/5)

2) прямая B1D и плоскость ABC

BB1 ⊥ (ABC) ⇒ BB1 ⊥ BD ⇒ BD  - проекция прямой B1D на плоскость ABC, а ∠B1DB- искомый угол.

Рассмотрим ΔB1DB (∠B=90°):

BB1=AA1=12

BD найдём из прямоугольного ΔABD(∠A=90°) по т.Пифагора:

BD² =AB²+AD²=25+49=74

tg ∠B1DB=BB1/BD=   = =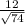

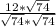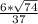
∠B1DB= arctg